مفهوم لیزر

لیزر یک نوسانگر اپتیکی است. در این نوسانگر همانند سایر نوسانگرها نظیر نوسانگر جسم و فنر متصل یا آونگ، جابجایی انرژی رخ‌ می‌دهد. جابجایی انرژی بین ماده و نور. در واقع این جابجایی انرژی بین ساختارهای کوانتومی ماده (که آنها را مولکول می‌نامیم) و میدان الکترومغناطیس روی می‌دهد. اگر بخشی از انرژی میدان الکترومغناطیس را از سیستم خارج کنیم، این نوسانگر به عنوان یک منبع نور عمل خواهد کرد. کمابیش همهٔ منابع نور طبیعی نیز به همین گونه عمل می‌کنند. اما نور حاصل از منابع نور لیزری با نور منابع معمولی متفاوت است. در این نور عمدهٔ ویژگی‌های نور و نحوهٔ انتشار آن کنترل شده است.

ویژگی‌های نور لیزری

خصوصیات زیر، نور لیزری را از نور سایر منابع متمایز می‌کند:

• تکفامی
• شدت بالا
• همدوسی (همبستگی فضایی و زمانی نور)
• نحوهٔ انتشار تنظیم‌شده (جهت‌دار بودن، موازی بودن)
• توزیع فضایی تنظیم‌شدهٔ شدت (وجوه تابشی مشخص)
• توزیع زمانی تنظیم‌شدهٔ شدت (رژيم تابشی مشخص)
• قطبش مشخص
• ...

هر نوری که بخشی از این شرایط را داشته باشد، نور لیزری نامیده می شود. بنابراین لیزری بودن صفتی است که به درجات مختلف به نور اطلاق می‌گردد. تکفامی و همدوسی از ویژگی‌های اصلی و مرتبط با هم هستند که نور بدون آنها نور لیزری نخواهد بود.

اجزای منابع نور لیزری

ساختار منابع لیزری را می‌توان به سه بخش اصلی تقسیم کرد:

• محیط فعال یا تقویت‌کنندهٔ نوری
• سیستم تحریک یا دمش
• حفره یا کاواک نوری

محیط فعال نور را تقویت می‌کند. به این منظور باید به محیط انرژی تزریق شود.

سیستم تحریک تزریق انرژی به داخل محیط را انجام می‌دهد. تحریک به روش‌های مختلفی انجام می‌شود. از جمله:

تحریک نوری، تحریک الکتریکی، تحریک شیمیایی و تحریک مکانیکی

حفرهٔ نوری کارکردهای زیر را دارد:

اعمال پس‌خوراند جهت نوسان‌سازی، انتخاب طول‌موج (وجوه طولی)، انتخاب نحوهٔ تابش و توزیع شدت (وجوه عرضی)

مهندسی نور در لیزرها

ویژگی‌های نور لیزری از طریق کنترل و تنظیم بخش‌های مختلف منبع نور لیزری حاصل می‌شود. مثلاً با تنظیم کاواک می‌توان طیف فرکانسی تابش را کنترل کرد.
گاهی با مهندسی چند جزء یا ترکیبی از آن‌ها می‌توان به ویژگی مورد نظر رسید. به عنوان مثال رژیم زمانی تابش را می‌توان هم با اعمال تغییر در محیط فعال، هم با نحوهٔ تحریک و هم با تغییر زمانی حفره کنترل کرد. ترکیبی از آنها نیز بکار گرفته می‌شود.
از سویی بخشی از ویژگی‌های لیزر را می‌توان با پردازش‌های بعدی نور خروجی تغییر داد، مثل تغییر طول‌موج تابشی با استفاده از فرآیند تولید هماهنگ دوم و یا تغییر حالت قطبش نور خروجی توسط قطبشگر.

دسته‌بندی منابع نور لیزری

لیزرها را به روش‌های مختلفی دسته‌بندی می‌کنند از جمله:

• تقسیم‌بندی بر اساس فاز محیط فعال (لیزرهای گازی، مایع و جامد)
• تقسیم‌بندی بر اساس توان تابشی (لیزرهای کم‌توان، لیزرهای قدرت و ...)
• تقسیم‌بندی بر اساس رژیم تابشی (پیوسته و پالسی)
• تقسیم‌بندی بر اساس نوع تحریک یا دمش انرژی
• تقسیم‌بندی بر اساس ناحیهٔ طول‌موج تابشی (لیزرهای مادون قرمز، مرئی، اشعه x و ...)
• تقسیم‌بندی بر اساس قابلیت تنظیم فرکانس

انواع منابع نور لیزری

با ترکیبی از دسته‌بندی‌های فوق، می‌توان دورنمایی از انواع منابع نوری لیزری را ارائه داد:

• لیزرهای گازی (مانند لیزرهای هلیوم-نئون، آرگون، کریپتون، نیتروژن، CO₂، CO، اگزایمر)
• لیزرهای جامد (مانند لیزرهای یاقوت Nd:YAG، Er:YAG، Ti:Saphire، Nd:Glass)
• لیزرهای رنگیزه‌ای (رودامین 6G، کورامین و ...)
• لیزرهای نیمه‌هادی (مانند لیزرهای دیودی مثل GaN, AlGaAs, InGaAsP)
• لیزرهای بخار فلز (مانند لیزر بخار مس، بخار کادمیوم، بخار جیوه، بخار سلنیوم و بخار طلا)
• لیزرهای دینامیک‌ گازی
• لیزرهای تار نوری
• لیزرهای بلور فوتونی
• لیزرهای شیمیایی (مانند لیزرهای HF, DF, COIL)
• لیزرهای الکترون آزاد
• لیزرهای زیستی

فیزیک لیزر

نور، انرژی الکترومغناطیسی است و تولید نور مستلزم تغییر در توزیع انرژی بین میدان‌های الکترومغناطیسی و ماده است. بنابراین برای فهم عملکرد منابع نور لیزری به عنوان مولد نور، ضروری است که فرمولبندی‌های فیزیکی از ماده و میدان‌های الکترومغناطیسی و نیز ویژگی‌های برهمکنش این دو بررسی شوند.

عموماً برهمکنش الکترومغناطیس با فرمولبندی «نظریه الکترومغناطیس» که نظریه‌ای کلاسیک است بیان می‌شود (برای مروری بر آن به درس مستقل نظریه الکترومغناطیس رجوع شود). این نظریه از مفهوم «میدان‌های الکترومغناطیس» برای توصیف برهمکنش استفاده می‌کند. اما این تنها فرمولبندی ممکن نیست. فرمولبندی کاملتر «نظریهٔ الکترودینامیک کوانتومی» است. برای توصیف کوانتومی نور باید میدان‌های الکترومغناطیس را کوانتیده کرد. اما اگر بخواهیم بدون پرداختن به آن، به توصیفی نه چندان کامل اما رضایتبخش اکتفا کنیم، می‌توان فرض کرد که نور از ذراتی با انرژی مشخص موسوم به «فوتون» تشکیل شده است. این ذرات را می‌توان بصورت موجی فشرده در زمان (بسته موج) و حاصل انتشار یک نوسان در آن بازهٔ زمانی با فرکانس مشخص در نظر گرفت. انرژی این ذرات به فرکانس یا طول موج آنها بستگی دارد.

از طرفی در چارچوب نظریهٔ الکترومغناطیس، بسیاری از رفتارهای الکتریکی و مغناطیسی ماده قابل فهم است. یکی از کلیدی‌ترین مفاهیم در این توصیف، مفهوم «ضریب شکست» است. بر اساس این مفهوم موضوعاتی چون تغییر در سرعت انتشار نور، نحوه انتشار نور در محیط‌های متفاوت (همگن، غیر همگن، همسانگرد و غیرهمسانگرد)، رفتار نور در مرز جدایی محیط‌های مختلف، پدیدهٔ پاشندگی، پدیدهٔ جذب و بسیاری از دیگر پدیده‌های اپتیکی بیان می شوند. اما این توصیف از ساختار ماده برای بیان عملکرد محیط فعال کفایت نمی‌کند.

برای توصیف ماده می‌توان مستقیماً به سراغ «مکانیک کوانتومی» رفت. در اینجا ماده از مجموعه آماری از ذرات تشکیل شده است. ذراتی که برای توصیف وضعیت آنها از مفهوم «حالت» استفاده می‌کنیم. حالت یک سیستم در ساده‌ترین وضعیت با انرژی ذره مشخص می‌شود. اگر دو حالت متمایز انرژی یکسان داشته باشند آنگاه کمیت‌های فیزیکی دیگر نظیر اندازه‌ حرکت زاویه‌ای به توصیف حالت اضافه می شود تا آنها را تفکیک کند. علاوه بر این معادلات مکانیک کوانتومی تحول زمانی حالت‌ها را نیز مشخص می‌کنند.

برهمکنش نور و ماده در واقع انتقال انرژی بین ماده و میدان (یا همان فوتون‌ها) است. این انتقال به دو صورت رخ می‌دهد:

• انتقال انرژی از میدان نور به ماده که به آن پدیدهٔ «جذب» می‌گوییم.


• انتقال انرژی از ماده به میدان که به آن پدیدهٔ «گسیل» می‌گوییم. در مورد مجموعه آماری از ذرات این پدیده به دو طریق ممکن است رخ دهد: یا ناشی از برهمکنش ماده با محیط یا میدان خلاء که به آن «گسیل خودبخود» می‌گوییم و یا ناشی از برهمکنش ماده با محیط یا میدان غیر خلاء که به آن «گسیل برانگیخته» گفته می‌شود.

در مورد برهمکنش ماده و نور، دو نکته حائز اهمیت است: نخست آنکه رفتار آماری محیط در اینجا نقش کلیدی خواهد داشت و ویژگی‌های آماری مثل فاز تجمعی محیط تأثیر گذار خواهد بود. دوم آنکه خود فرآیند انتقال نیز جالب توجه است. این فرآیند در هر مورد در یک بازه زمانی خاص اتفاق می‌افتد و تغییر میدان و ماده در بازهٔ زمانی برهمکنش حائز اهمیت است.

در مجموع می‌توان برای توصیف برهمکنش محیط مادی و نور دو نظریهٔ الکترومغناطیس و مکانیک کوانتومی را به ترتیب برای توصیف نور و ماده بکار گرفت و با در هم آمیختن آنها نظریه‌ای «نیمه کلاسیک» ساخت. بر این اساس بسیاری از پدیده‌های لیزر، اما نه همهٔ آنها، قابل فهم خواهند بود. اما یک «نظریهٔ لیزر» کامل را تنها در چارچوب الکترودینامیک کوانتومی می‌توان بنا کرد.

وارونی جمعیت

مکانیک کوانتومی توصیفی کامل از حالت اتم و مولکول و تغییر این حالات در برهمکنش آنها با نور ارائه می‌دهد. پدیده‌هایی همچون «جذب»، «گسیل» و «پراکندگی» بیان‌کننده این تغییر حالت است. در عمل ما بندرت با یک یا چند اتم یا مولکول سروکار داریم و عموماً با تعداد بسیار زیادی اتم (در حد چند مول) مواجه هستیم. بنابراین لازم است که اصول مکانیک کوانتومی را در مورد «مجموعه‌های آماری» از اتم‌ها و مولکول‌ها اعمال کنیم.

نحوهٔ کنار هم قرار گرفتن این تعداد زیاد ذره، رفتار تجمعی آنها را تعیین می‌کند. اگر چه این رفتار برخاسته از رفتار تک تک اتم‌ها و مولکول‌ها می‌باشد اما ویژگی‌های جدیدی نیز بروز خواهد کرد. برای شروع کار فرض می‌کنیم که ذرات با حداقل برهمکنش در کنار یکدیگر قرار گرفته‌اند. به بیان دیگر مجموعه آماری ذرات در فاز یا حالت تجمعی «گاز» قرار دارند. در فاز گاز، ذرات تقریباً آزادانه و مستقل حرکت می‌کنند. زمانی که فاصلهٔ بین دو ذره آنقدر کم شود که برهمکنش بین آنها مسیر حرکت ذره را عوض کند، می‌گوییم بین دو یا چند مولکول برخورد رخ داده است. در برخورد، برهمکنش الکترومغناطیس بین اجزای مولکول‌های برخوردکننده باعث می‌شود حالت کوانتومی هر مولکول نیز عوض شود. در حالت گاز، مدت زمانی که هر مولکول در وضعیت برخورد قرار دارد بسیار کوچکتر از زمان کل حرکت آن است. به عبارت دیگر برخوردها بندرت و گاه‌گاه رخ می‌دهند. اگر تعداد ذرات در یک حجم مشخص زیاد شود، تعداد برخوردها هم افزایش می‌یابد و گاز به «گاز چگال» تبدیل می‌شود. اگر زمان برخوردها خیلی زیاد شود، دیگر نمی‌توان مولکول‌ها را آزاد فرض کرد. آنها همواره درگیر خواهند بود. ترکیبی از مولکول‌ها در حالت برخورد دائم را «فاز تجمعی جامد» می‌نامند. در این حالت ذرات (اتم‌ها، مولکول‌ها یا یون‌ها) بسیار مقید شده و حتی توزیع فضایی آنها به نقاط خاصی از فضا (موسوم به شبکه بلوری) محدود خواهد شد.

برای بررسی رفتار تجمعی ذرات از یک مجموعهٔ آماری ذرات در فاز تجمعی گاز شروع می‌کنیم. این ذرات در یک محفظه با ابعاد مشخص قرار دارند. انرژی هر یک از این ذرات را می‌توان به سه بخش عمده تقسیم کرد:

الف) انرژی انتقالی. ذرات با سرعت نسبتاً زیاد در جهات مختلف فضا حرکت می‌کنند. هیچ جهتی مرجح نیست. بر اثر برخورد دو یا چند ذره با یکدیگر جهت حرکت آنها تغییر خواهد کرد. میانگین آماری انرژی جنبشی انتقالی این ذرات را «دمای گاز» می‌نامیم. به عبارت دیگر هرچه سرعت حرکت ذرات بیشتر باشد، دمای گاز زیادتر است. با افزایش سرعت، تعداد برخوردها در واحد زمان هم افزایش می‌یابد. در اغلب حالات، دمای گاز همان چیزی است که به عنوان دمای ماکروسکوپی با دماسنج اندازه‌گیری می‌شود.

ب) انرژی نوسانی. اتم یا مولکول معمولاً از اجزای دیگری تشکیل شده است که به هم مقید هستند و موقعیت و توزیع فضایی‌شان به تعادل رسیده است. این اجزاء می‌توانند حول نقطه تعادل نوسان کنند. هر اتم یا مولکول حالات نوسان داخلی مشخصی دارد که بر اساس نظریهٔ مکانیک کوانتومی می‌توان حالات پایای نوسانی آن و انرژی‌های مربوطه را پیدا کرد. اختلاف انرژی حالات نوسانی معمولاً کوچکتر از اختلاف انرژی حالات الکترونی اتم یا مولکول است. میانگین انرژی جنبشی نوسانی مولکول‌ها را «دمای نوسانی گاز» می‌نامیم.

ج) انرژی دورانی. به تغییر جهت‌گیری مولکول در فضا نیز می‌توان انرژی نسبت داد. حالات دورانی پایای مولکول از بررسی کوانتومی آن بدست می‌اید. میانگین انرژی جنبشی دورانی مولکول‌ها را «دمای دورانی گاز» می‌نامند.

در برخورد دو مولکول با هم، آن دو به هم نزدیک می‌شوند. این نزدیکی باعث تغییر برهمکنش‌های الکترومغناطیس بین دو ذره، تغییر موقت هامیلتونی برهمکنش، ناپایدار شدن لحظه‌ای حالات پایای سیستم و در نتیجه تغییر حالت مولکول پس از برخورد می‌شود. به عبارت دیگر در اثر برخورد، انرژی یک مولکول ممکن است بیشتر شود و انرژی مولکول دیگر کمتر. البته در برخورد بخشی از انرژی هم ممکن است به شکل‌های دیگری ظاهر شود. مثلاً باعث افزایش یا کاهش سرعت انتقالی ذره گردد. در اثر برخورد توزیع انرژی مولکول بین انرژی انتقالی، نوسانی و دورانی تغییر می‌کند. پس از مدتی برخوردها باعث رسیدن به حالت تعادل ترمودینامیکی بین ذرات خواهند شد. این برخوردها باعث می‌شوند که میانگین انرژی جنبشی انتقالی، نوسانی و دورانی با هم برابر شود. یعنی می‌توان همان «دما»ی متعارف ترمودینامیکی را برای توصیف سیستم بکار گرفت. بنابراین فعلاً دماهای نوسانی و دورانی را فراموش کرده و مگر در حالات خاص غیرتعادلی تنها دمای مرتبط با حرکت انتقالی ذرات را در نظر می‌گیریم.

همانگونه که اشاره شد، برخورد ذرات باعث انتقال انرژی بین حرکت انتقالی آنها و حالت کوانتومی ذره می‌شود. اگر این برخوردها نبود، بدلیل برهمکنش مولکول‌ها با محیط خلاء کوانتومی و پدیدهٔ گسیل خودبخود، همهٔ مولکول‌ها در حالت کوانتومی پایه با کمترین مقدار انرژی قرار می‌گرفتند. بعبارت دیگر توزیع مولکول‌ها در حالت کوانتومی بگونه‌ای بود که صد در صد آنها در حالت پایه قرار داشتند. به این حالت «صفر مطلق» می‌گویند. سیستم در این وضعیت حداقل انرژی را دارد. دمای صفر را به این حداقل حالت نسبت می‌دهند. طبیعتاً این حالت دست‌نیافتنی است. اما در حالت طبیعی برخوردها باعث می‌شوند که مولکول‌ها در حالات پایای کوانتومی متفاوتی توزیع شوند. نحوهٔ این توزیع چگونه است؟ به عبارت دیگر اگر فرضاً یک مول مولکول داشته باشیم، چند درصد آنها در حالت شماره ۱ باانرژی \(E_1\)، چند درصد در حالت پایای دوم با انرژی \(E_2\) و به همین ترتیب چند درصد در حالات با انرژی بالاتر قرار می‌گیرند؟ این توزیع تعادلی مولکول‌ها در حالات پایای انرژی مختلف را می‌توان با توزیع آماری بولتزمان نشان داد که بصورت زیر بیان می‌شود: \[p_i\propto e^{-E_i/kT}\] که در اینجا \(p_i\) ، نشان‌دهندهٔ احتمال یافتن ذره در حالت شمارهٔ \(i\) با انرژی \(E_i\) است. شکل توزیع نمایی است و نشان می‌دهد که با افزایش انرژی شانس داشتن آن انرژی کم می شود. از طرفی هر چه دما افزایش یابد، شانس داشتن انرژی‌های بالاتر بیشتر می شود. با توجه به این توزیع احتمالی می‌بینیم که اتم‌ها یا مولکول‌ها به نحوی در ترازهای مختلف انرژی توزیع خواهند شد که در تمامی شرایط همواره تعداد مولکول‌هایی که می‌توانند انرژی بالاتری داشته باشند از تعداد مولکول‌های با انرژی پایین‌تر کمتر است. به عبارت دیگر اگر مولکول‌های با یک حالت انرژی مثل \(E_i\) را جدا کنیم خواهیم دید که تعداد آنها با افزایش انرژی حالت مورد نظر کم خواهد شد. به تعداد مولکول‌های با انرژی یک حالت مشخص «جمعیت» آن حالت یا «جمعیت تراز» می‌گوییم.

بنابراین در هر دمای تعادلی ترمودینامیکی خاص، توزیع جمعیتی مشخصی از مولکول‌ها در ترازهای انرژی آن مولکول خواهیم داشت که بر اساس توزیع بولتزمان تعیین می‌شود. این توزیع جمعیتی بشدت نامتقارن است و با افزایش انرژی حالت بطور نمایی کاهش می‌یابد. اما هر چه دما بیشتر شود، این توزیع به سمت توزیع یکنواخت‌تر متمایل خواهد شد. در دماهای پایین عمدهٔ جمعیت مولکولی در ترازهای پایه و اولین حالت‌های برانگیخته پخش شده‌اند و شانس پیدا کردن مولکولی در حالت‌های با انرژی زیاد فوق‌العاده ناچیز است. نمونه توزیع در دماهای مختلف را می‌توانید در شکل ببینید. در این شکل‌ها می‌بینید که فرضاً ۱۰۰۰ مولکول چگونه در بین چندین تراز انرژی مولکول توزیع می‌شوند. طول خط مربوط به هر تراز متناسب با جمعیت آن است و منحنی خط‌چین روند نظری تغییر این طول یعنی همان توزیع بولتزمان را نشان می‌دهد.

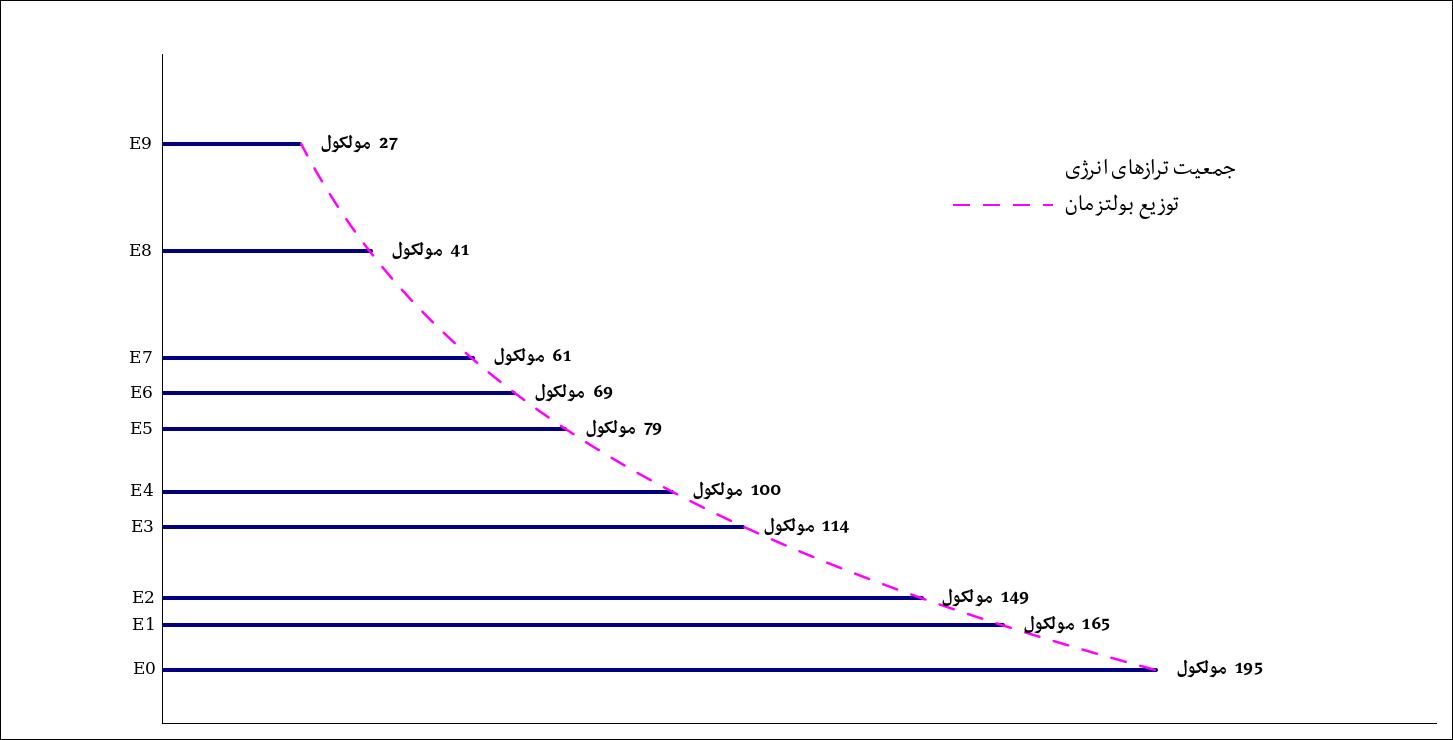در شکل بعد، وضعیت در دمای بالاتری نشان داده شده است. دیده می‌شود که شانس حضور مولکول‌ها در ترازهای بالا بیشتر شده است.

و نهایتاً این شکل مربوط به دمای نسبتاً پایین است که عمدهٔ مولکول‌ها در سه تراز اول توزیع شده‌اند و ترازهای بالا خالی از جمعیت می‌باشند.

ویژگی جالب توزیع بولتزمان، برقراری ارتباط بین میانگین انرژی جنبشی انتقالی مولکول‌ها از یک طرف و توزیع آنها در حالات کوانتومی از طرف دیگر است.

یک مولکول با دو حالت مجاز انرژی پایا را در نظر بگیرید. چیزی که به آن اصطلاحاً «سیستم دوترازه» گفته می‌شود. رفتار مجموعهٔ آماری از این مولکول را بررسی می کنیم. فرض کنید در ابتدای کار فقط یک مولکول در محیط محصورمان داریم. اگر این مولکول در تراز پایه باشد و فوتونی با انرژی معادل اختلاف دو تراز به محیط بتابانیم شانس خوبی وجود دارد که «جذب» رخ دهد و مولکول به تراز بالاتر برود. اگر در ابتدا مولکول در تراز بالا (حالت برانگیخته) باشد و فوتون بموقع یعنی قبل از گسیل خودبخود با مولکول برخورد کند، گسیل برانگیخته روی خواهد داد و فوتون دیگری مشابه فوتون اول ظاهر خواهد شد. بنابراین تاباندن یک فوتون به این سیستم تک مولکولی برانگیخته باعث می‌شود در خروجی دو فوتون داشته باشیم. حال فرض کنید به جای یک مولکول تعداد زیادی مولکول وجود داشته باشد. این مولکول‌ها بر اساس توزیع بولتزمان بین تراز پایه و تراز برانگیخته توزیع می‌شوند. به عنوان مثال ۹۰ درصد مولکول‌ها در حالت پایه و ۱۰ درصد آنها در حالت برانگیخته هستند. در اینجا اگر فوتونی وارد محفظه شود شانس جذب آن بمراتب بیشتر از شانس گسیل برانگیخته یک فوتون دیگر است، چون تعداد مولکول‌های در حالت پایه بمراتب بیشتر از مولکول‌های حالت برانگیخته است و شانس جذب و شانس گسیل به جمعیت ترازهای بالا و پایین وابسته است. بنابراین در خروجی هیچ فوتونی نخواهیم داشت. اگر بجای یک فوتون دهها فوتون هم بفرستیم، باز هم تعداد فوتون‌هایی که خارج می‌شوند کمتر خواهد بود یعنی در عبور نور از محیطی جاذب، شدت نور خروجی کاهش خواهد یافت و همواره تضعیف خواهیم داشت.

حال فرض کنید به یکباره تعداد بسیار زیادی فوتون را به داخل محفظه بفرستیم، بسیاری از آنها جذب خواهند شد. جذب آنها منجر به افزایش جمعیت تراز بالا و کاهش جمعیت تراز پایین می‌شود. یعنی در مثال فوق جمعیت تراز پایه کمتر از ۹۰ درصد و جمعیت تراز بالا بیش از ۱۰ درصد خواهد شد. بتدریج با تغییر جمعیت شانس جذب کم شده و شانس گسیل برانگیخته بیشتر خواهد شد. البته نباید فراموش کرد که گسیل خودبخود هم همزمان منجر به کاهش جمعیت تراز بالا خواهد شد و بر احتمالات مربوطه تأثیر می‌گذارد.

سؤالی که پیش می‌آید این است: آیا می‌توان با افزایش شدت نور تابشی به داخل محیط کاری کرد که جمعیت تراز بالا بیشتر از تراز پایین شود؟ پاسخ برای این سیستم دو ترازه خیر است. دقت کنید که با افزایش جمعیت تراز بالا و افزایش شانس گسیل برانگیخته چون تعداد کل مولکول‌ها ثابت است، جمعیت تراز پایین و شانس جذب کم می‌شود. در این حالت تعداد مولکول‌هایی که در واحد زمان بدلیل گسیل برانگیخته از تراز بالا به پایین می‌آیند افزایش می‌یابد ولی همزمان تعداد مولکول‌هایی که بدلیل جذب بالا می‌رفته‌اند کم می‌شود. این امر نهایتاً منجر به کاهش جمعیت تراز بالا و افزایش مجدد جمیعت تراز پایین خواهد شد. پس همواره تعداد فوتون‌های خروجی کمتر از تعداد فوتون‌های ورودی خواهد بود و محیط «تضعیف‌‌کننده» یا «جاذب» باقی خواهد ماند. در‌واقع حدی‌ترین حالتی که می‌توان به آن دست یافت این است که جمعیت دو تراز مساوی شوند، ۵۰ درصد مولکول‌ها در تراز بالا و ۵۰ درصد آنها در تراز پایین قرار بگیرند. در این وضعیت محیط «شفاف» خواهد شد. همان مقدار فوتونی که به آن وارد شده است، از آن خارج می شود. به عبارت دیگر با بالابردن شدت نور توانسته‌ایم جذب در محیط را از بین ببریم. به این وضعیت اصطلاحاً «شفافیت القاء شده» می‌گویند.

حال فرض کنید به روشی سیستم را از حالت تعادل ترمودینامیکی خارج کنیم. مثلاً تعداد زیادی الکترون را با انرژی مناسب به داخل محیط پرتاب کنیم به نحوی که در برخورد آنها با مولکول‌ها، جمعیت تراز بالا به نحو قابل ملاحظه‌ای زیاد شود. به عنوان مثال ۷۰ درصد مولکول‌ها در تراز بالا و ۳۰ درصد آنها در تراز پایین باشند. این حالت غیر تعادلی است و طبیعی است که توزیع بولتزمان در اینجا صادق نیست. در این حالت اگر فوتونی وارد سیستم شود، شانس گسیل برانگیخته بیشتر است و عملاً ممکن است دو فوتون خارج شود. اگر تعداد زیادتری فوتون بتابانیم، تعداد فوتون‌ها در خروجی بیشتر خواهد بود. یعنی شدت نور در عبور از این محیط زیاد می شود. به چنین محیط‌هایی «محیط تقویت‌کننده» نور یا «محیط فعال» می‌گویند. داشتن محیط فعال منوط به آن است که جمعیت ترازهای با انرژی بالا بیشتر از جمعیت ترازهای با انرژی پایین باشد. این موضوع در تضاد با توزیع تعادلی بولتزمان است به همین دلیل به آن «وارونی جمعیت» می‌گویند. وارونی جمعیت شرط ایجاد محیط فعال است. وارونی جمعیت ایجاد شده در مثال بالا دوام نخواهد داشت. با‌ گذشت زمان و افزایش فوتون‌ها بر اثر گسیل برانگیخته، تراز بالا تخلیه می‌شود و تراز پایین پر خواهد شد و در فاصلهٔ کوتاهی وارونی جمعیت از بین رفته و محیط دوباره جاذب خواهد شد. برای حفظ فعال بودن محیط لازم است که عامل بیرونی (نظیر جریان الکترون‌ها) مرتباً تراز بالا را جمعیت‌دار کند. به این عمل اصطلاحاً دمش یا پمپاژ انرژی به داخل سیستم یا بطور خلاصه «دَمِش» می‌گویند. طبیعی است که دمش انرژی به داخل محیط باید متناسب با ترازهای انرژی و حساب شده باشد تا بتواند وارونی جمعیت بین دو تراز را حفظ کند.

اگر اصرار داشته باشیم توزیع بولتزمان را برای چنین سیستمی در نظر بگیریم، باید فرض کنیم که دمای مطلق سیستم منفی است تا در توزیع بولتزمان جمعیت تراز با انرژی بالاتر بیشتر از جمعیت تراز با انرژی کمتر بشود. یعنی محیط‌های فعال را می‌توان به عنوان سیستم‌های با دمای مطلق منفی در نظر گرفت. دقت کنید در اینجا اگر چه دما منفی است اما سیستم گرمتر از دمای صفر است یعنی انرژی آن از انرژی سیستم در دمای صفر مطلق بیشتر است.

به سراغ سیستم‌های واقعی‌تر «چند ترازه» می‌رویم. در این سیستم‌ها گذارهای جذبی و گسیلی متعددی بین ترازهای مختلف امکان‌پذیر است. البته بعضی از این گذارها بدلیل نقض قوانین بقا ممکن است ممنوع یا بسیار غیر محتمل باشند اما بسیاری از گذارها نیز مجاز هستند. گذارهای مجاز با شانس و احتمال‌های متفاوت رخ می‌دهند. در این سیستم‌ها برای ایجاد وارونی جمعیت لازم نیست که توزیع جمعیتی بین همهٔ ترازها معکوس شود. واورنگی جمعیت بین هر دو تراز می‌تواند منجر به فعال شدن محیط در طول موج یا فرکانس متناظر با آن گذار شود. دو نمونه از وارونگی جمعیت بین ترازهای مختلف در یک سیستم چند ترازه را می‌توان در شکل روبرو دید. در این شکل، جمعیت ترازهای 1 و 2 بیش از تراز پایه است و وارونی جمعیت وجود دارد.

به همین ترتیب بصورتی دیگر می‌توان وارونی جمعیت بین ترازهای ۳ و ۲ را در این شکل دید.

لیزر به عنوان تقویت‌کننده نور و یا مولد نور عمل می‌کند. لازمهٔ این تقویت، داشتن محیط فعال است و ایجاد محیط فعال هم متکی به وارونی جمعیت است. روش‌های ایجاد وارونی جمعیت یا همان دمش موضوع مبحث بعدی است.

موضوع تکمیلی: لیزرهای بدون وارونی جمعیت

اشاره شد که برای داشتن لیزر نیاز به ایجاد وارونی جمعیت است. آیا به طریق دیگری هم می‌توان عمل کرد؟ در‌واقع وارونی جمعیت ضروری است اما برای این کار نیاز نیست که در واقعیت امر هم جمعیت تراز پایین کمتر از جمعیت تراز بالا باشد. می‌توان بگونه‌ای عمل کرد که بخش بزرگی از جمعیت تراز پایین در فرآیند جذب و گسیل دخالت نکنند. در این حالت «جمعیت مؤثر» تراز پایین کمتر از جمعیت تراز بالا خواهد بود اما جمعیت واقعی بمراتب بیشتر است. یعنی وارونی جمعیت نداریم. چگونه می‌توان این کار را انجام داد؟ روش‌های متعددی وجود دارد. به عنوان نمونه می‌توان بخش بزرگی از مولکول‌های تراز پایین را سرگرم کرد. با افزودن مولکول دیگری به محیط که یک تراز انرژی هم‌سطح با تراز پایین مولکول اصلی داشته باشد، می‌توان در برخوردها نوعی تبادل انرژی بین این دو نوع مولکول برقرار کرد و مولکول‌های اصلی را از مشارکت در فرآیند جذب و گسیل بازداشت. به چند الگوی مختلف این کار امکان‌پذیر است که در جای خود باید مورد بحث قرار گیرد.

سازوکارهای دمش

برای ایجاد وارونی جمعیت بین دو تراز لازم است که به محیط انرژی تزریق شود. این تزریق انرژی باید حساب‌شده باشد. به عنوان مثال اگر انرژی حرارتی به سیستم بدهیم، تنها دمای آن افزایش خواهد یافت که نشان دهندهٔ توزیع تعادلی انرژی بین ترازهای مختلف است. جمعیت ترازهای بالا افزایش خواهد یافت اما وارونی جمعیتی بوجود نخواهد آمد. در‌واقع نتیجهٔ تزریق انرژی گرمایی متعادل شدن و برابر شدن جمعیت‌‌هاست نه وارونی جمعیت. بنابراین باید بطور گزینشی انرژی پاره‌ای از مولکول‌ها را افزایش داد. راههای مختلفی برای اینکار وجود دارد که در اینجا فهرست‌وار به آن‌ها اشاره می‌شود.

• دمش الکترونی
  اگر باریکه‌ای از الکترونها را از داخل محیط عبور دهیم، الکترون‌ها در برخورد با مولکول‌ها می‌توانند آن‌ها را به تراز بالاتر انرژی انتقال دهند. این روش بخصوص برای محیط‌های گازی مناسب است. برای اینکار باید انرژی جنبشی الکترونها به نحوی انتخاب شود که سطح مقطع برخورد برای فرآیند مورد نظر بیشینه باشد. از آنطرف باید عوامل دیگر محیط نیز مساعد باشند. بخصوص به فشار گاز باید اشاره کرد. به نحوی که برخوردهای بعدی بین مولکول‌ها، آن‌ها را به سرعت به حالت پایه برنگرداند. معمولاً چگالی و فشار بهینه‌ای وجود دارد. علاوه بر این می‌توان به محیط انواع دیگر مولکول‌ها را اضافه کرد تا به حالت ایده‌آل رسید. برای تولید باریکه الکترونی، کاتدی که در یک سوی محیط حرارت داده می‌شود، الکترون‌های لازم را تولید خواهد کرد. اتصال آند در سوی دیگر محیط که تحت ولتاژ مثبت قرار دارد، به الکترون‌ها شتاب داده و جهت حرکت آن‌ها را تعیین خواهد کرد. انرژی جنبشی الکترون‌ها را می‌توان با انتخاب ولتاژ بین کاتد و آند در دو سر محیط تغییر داد.
  نوع دیگر دمش الکتریکی، اعمال ولتاژ به دو سر یک اتصال نیمه‌هادی است که منجر به ایجاد حاملین بار (حفره یا الکترون) اضافه می‌شود که به نوبهٔ خود می‌توانند مولکول‌های آن نیمه‌هادی را تحریک کنند. می‌توان شرایط مناسب برای ایجاد وارونی جمعیت را فراهم کرد. در اینجا جریان الکتریکی در محیط نیمه‌هادی نقش باریکهٔ الکترونی را خواهد داشت.


• دمش با تخلیه الکتریکی
  اگر ولتاژی بالاتر از ولتاژ شکست الکتریکی محیط به دو طرف محیط اعمال شود، تخلیه الکتریکی رخ خواهد داد. این تخلیه الکتریکی بهمنی از الکترون ایجاد خواهد کرد. این الکترونها می‌توانند در برخورد با مولکول‌ها به آنها انرژی انتقال دهند. این تخلیه عموماً در محیط‌های گازی بکار می‌رود. بسیاری از لیزرهای گازی نظیر لیزر دی‌اکسید کربن و لیزر هلیوم-نئون با این روش پمپاژ می‌شوند. زیرا این محیط‌ها قادرند در فاصلهٔ کوتاهی تخریب محیط ناشی از تخلیه الکتریکی را جبران کنند. ایجاد یک تخلیه الکتریکی یکنواخت هم ضروری است و هم مشکل.
  دو نوع تخلیه الکتریکی متداول وجود دارد:
  
  
  • تخلیه تابشی (Glow discharge). در این‌ نوع تخلیه بر اثر عبور جریان یک پلاسما ایجاد می‌شود. اگر ولتاژ اعمالی مناسب باشد، این پلاسما می‌تواند خودش را حفظ کند و حتی با کاهش ولتاژ و اعمال ولتاژی زیر حد ولتاژ شکست حالت پایداری داشته باشد. این تخلیه همراه با تابش الکترومغناطیس همراه است و به همین دلیل به آن تخلیه تابشی گفته می‌شود. ناحیهٔ طیفی تابش به نوع گاز و فشار آن بستگی دارد. به دلیل تابش نور، تخلیه تابشی یکی از مکانیزم‌هایی است که از آن برای تولید منابع نور متعارف استفاده می‌شود. لامپ‌های فلوئورسنت (مهتابی) از این دسته هستند. طیف تابشی آنها در ناحیه ماوراء بنفش است و معمولاً یک لایهٔ فلوئورسانس نور آنها را به ناحیهٔ مرئی تبدیل می‌کند. به عنوان نمونهٔ دیگر می‌توان از لامپ‌های نئون تبلیغاتی و صفحات نمایش و تلویزیون‌های پلاسما نام برد.
    دقت کنید که تابش نوری که در اینجا ایجاد می‌شود در دمش انرژی برای ایجاد وارونی جمعیت نقشی ندارد. تزریق انرژی از طریق الکترون‌هاست.
  
  
  • تخلیه هاله‌ای یا کُرونا (Corona discharge). اگر یک هادی باردار داشته باشیم، محیط اطراف آن ممکن است یونیزه شود. این امر بخصوص هنگامی که محیط اطراف، سیالی مانند یک گاز است محتمل‌تر خواهد بود. این حالت وقتی رخ می‌دهد که ولتاژ آنقدر بالا هست که باعث ایجاد یک ناحیهٔ هادی در محیط اطراف آن فلز باردار شود، اما بحدی افزایش پیدا نکرده است که باعث تخلیه الکتریکی شود. بنابراین محیط اطراف فلز یونیزه شده است اما شکست الکتریکی رخ نداده است. اطراف لبه‌های تیز بدلیل افزایش شدت میدان الکتریکی این امر بیشتر مشاهده می‌شود. معمولاً محیط یونیزه شده تابش هم دارد. این تابش بصورت هاله یا کرونایی اطراف هادی ظاهر خواهد شد. در بسیاری از کاربردهای الکتریکی، کُرونا عامل مزاحمی است که باعث اتلاف انرژی می‌شود و سعی در کاهش آن با کم کردن لبه‌های تیز و نیز استفاده از عایق‌های مناسب می‌شود. امّا کرونای کنترل شده کاربردهای متعددی دارد. استفاده از تخلیه هاله‌ای برای دمش لیزرهای گازی متداول است. گاهی در لیزر نیتروژن و نیز لیزر دی‌اکسید کربن از این روش استفاده می شود. با توجه به اینکه در این حالات باید بتوان یک تخلیه هاله‌ای یکنواخت در محیط ایجاد کرد و اینکار در طول محیط مشکل است، معمولاً تحریک الکتریکی عرضی استفاده می‌شود.


• دمش رادیویی
  در این روش با قرادادن محیط در معرض امواج الکترومغناطیس رادیویی با توان بالا و انرژی مناسب، عمل فعال‌سازی محیط رخ می‌دهد. در این موارد گاز محصور در یک محفظه بسته مورد تابش قرار می‌گیرد و نیازی به الکترود نیست.


• دمش نوری
  در این روش به محیط نور تابانده می‌شود. فرکانس نور باید به نحوی باشد که انرژی آن مناسب بوده و بتواند در محیط وارونی جمعیت بوجود آورد. انتقال انرژی بر اساس پدیدهٔ جذب است. واضح است که در یک سیستم دوترازه هیچ‌گاه نمی‌توان با روش دمش نوری به وارونی جمعیت رسید. چون همانطور که قبلاً در بحث وارونی جمعیت دید در چنین محیط‌هایی حداکثر می‌توان به تعادل جمعیت بین دو تراز رسید. بنابراین در دمش نوری لازم است که حتماً از سه یا چند تراز ماده استفاده شود. دمش نوری بخصوص در لیزرهای حالت جامد کاربرد دارد. در این محیط‌ها تخلیه الکتریکی بسیار مشکل است. اولاً حرکت الکترون‌ها در آن‌ها بسیار محدود است و از طرفی اگر تخلیه الکتریکی رخ دهد، محیط قدرت بازسازی ندارد (اصطلاحاً محیط می سوزد یعنی ساختارش به نحوی تغییر می‌کند که قابل ترمیم نیست.). دمش نوری در لیزرهایی چون لیزر یاقوت و لیزر بلور نئودیمیوم-یاگ (Nd:YAG) استفاده می‌شود. برای دمش نوری از منابع نور مختلفی استفاده می‌شود. از انواع فلاش‌های نوری که پالسهای نوری مختلفی را تولید می‌کنند گرفته تا استفاده از یک لیزر دیگر برای تحریک نوری. به عنوان نمونه در یک لیزر رنگ که محیط فعال از رنگدانه‌های مختلف در فاز مایع تشکیل می‌شود، محیط را با تابش نور از منبع لیزری مانند Nd:YAG تحریک می‌کنند. خود لیزر Nd:YAG هم توسط دمش نوری از طریق یک فلاش تحریک نوری می‌شود.


• دمش شیمیایی
  در یک واکنش شیمیایی محصولات اولیه با هم ترکیب شده و محصولات نهایی را بوجود می‌آورند. در این واکنش‌ها ممکن است انرژی گرفته شده یا آزاد شود. احتمال دارد محصولات واکنش بدلیل انرژی آزاد شده در حالات برانگیخته قرار گیرند. در صورت طراحی مناسب می‌توان شرایطی را بوجود آورد که توزیع انرژی در مولکول‌های تولید شده در واکنش شیمیایی در حالت وارونی جمعیت باشند. بدلیل سمیّت بالای اغلب مواد مورد استفاده در لیزرهای شیمیایی و پیچیدگی کار با آنها، این روش متداول نیست. امّا امتیاز لیزرهای شیمیایی امکان دریافت انرژی بالا از آنهاست. در‌واقع این لیزرها یکی از سه کاندید اصلی تولید لیزرهای با توان بسیار بالا هستند. این توان بالا معمولاً کارکرد تخریبی دارد و به همین دلیل کاربرد اصلی آن‌ها کاربردهای نظامی و ساخت سلاح‌های لیزری است. توان تولیدی پیوستهٔ این لیزرها ممکن است تا مگاوات برسد. نمونهٔ کلاسیک این لیزرها، لیزر فلورید هیدروژن (HF) و فلورید دوتریوم (DF) است. نمونهٔ کاملتر آن لیزر موسوم به لیزر COIL (لیزر شیمیایی اکسیژن-ید) است. اغلب لیزرهای شیمیایی در ناحیهٔ مادون قرمز انرژی تولید می‌کنند. لیزرهای COIL قادرند تا چند مگاوات انرژی پیوسته نورانی ایجاد کند. این لیزر قابل ساخت در مقیاس‌های توان پایین‌تر هم هست و به همین دلیل در محدوده‌های چند ده کیلوواتی می‌تواند بدیلی برای لیزرهای جوشکاری و برش مانند لیزرهای دی‌اکسیدکربن باشد. البته سمیّت گازهای ید و کلر بکار رفته در آنها یک مانع جدی در کاربرد این لیزرهاست. بنظر می‌رسد علاقه سیستم‌های نظامی کشورهای مختلف به این لیزرها کاهش پیدا کرده است و به همین دلیل ساخت و توسعه لیزرهای شیمیایی متوقف شده است. واضح است که این امر نشانهٔ کاهش خوی خشونت‌ورزی انسان نیست بلکه احتمالاً بدلیل یافتن بدیل‌های کارآمدتر و خشن‌تر بوده است.


• دمش مکانیکی
  این روش دمش چندان متداول نیست اما بطور خاص در «لیزرهای دینامیک گازی (GDL)» مورد استفاده قرار می‌گیرد. در این روش وارونی جمعیت ناشی از «انبساط بی‌دررو» مخلوطی از گازهاست. در ابتدا مخلوطی از گازهای داغ با انرژی بالا تولید می‌شود. این مخلوط قرار است محیط لیزری را تشکیل دهد. خود این گاز داغ ممکن است حاصل از احتراق باشد. احتراق نه تنها به سیستم انرژی تزریق می‌کند و دمای بالای گاز را تأمین می‌کند، بلکه سوختن سوخت مناسب می‌تواند ترکیب گازهای لازم برای سیستم را نیز تأمین کند. در این وضعیت ترازهای بالای انرژی بدلیل دمای بالا جمعیت‌دار شده‌اند. برای ایجاد وارونی جمعیت، گاز داغ از یک «شیپورهٔ مافوق صوت» عبور داده می‌شود. این شیپوره باعث انبساط یکبارهٔ گاز می‌شود. سرعت انبساط باعث می‌شود بتوان آن را بی‌دررو در نظر گرفت. قبل از انبساط، ترازهای انرژی مورد نظر (عموماً ترازهای نوسانی و یا دورانی) در حال تعادل ترمودینامیکی با دمای انتقالی گاز هستند و بنابراین پرجمعیت می‌باشند. انبساط ناگهانی گاز در عبور از شیپوره باعث افت شدید دمای انتقالی گاز می‌شود اما ترازهای نوسانی فرصت نمی‌کنند که با دمای انتقالی به تعادل برسند بنابراین دمای بالاتری را حس کرده و در مدت زمان نسبتاً قابل قبولی جمعیت‌دار خواهند ماند. این امر منجر به ایجاد وارونی جمعیت خواهد شد. به عنوان نمونه می‌توان به لیزر دینامیک گازی دی‌اکسیدکربن اشاره کرد که قادر است در ناحیهٔ مادون‌قرمز، خروجی تابشی پرتوانی تا چند صد کیلووات را فراهم کند. این لیزرها نیز عموماً در سیستم‌های نظامی و دفاعی بکار گرفته می‌شوند.


• دمش با تفکیک مولکولی
  از روش‌های قدیمی ایجاد وارونی جمعیت است که در آن مولکول‌هایی که در ترازهای انرژی پایین قرار دارند جدا شده و از محیط خارج می شوند. این امر منجر به افزایش نسبی تعداد مولکول‌های تراز بالا نسبت به تراز پایین خواهد شد. نمونهٔ این نوع دمش در نمونه‌های اولیهٔ لیزر آمونیاک (با تابش در ناحیهٔ میکروویو موسوم به «میزر») بکار گرفته شده است. این روش در ناحیه طیفی مرئی کاربرد زیادی ندارد، چون در ناحیهٔ امواج میکروویو \(h\nu\ll kT\) است و توزیع جمعیت بگونه‌ای است که اختلاف جمعیت ترازهای بالا و پایین چندان زیاد نیست. در نتیجه بیرون بردن مولکول‌های تراز پایین باعث وارونی جمعیت قابل ملاحظه‌ای می‌شود. اما در ناحیه امواج مرئی، که \(h\nu\gg kT\) است، عمدهٔ جمعیت در تراز پایه است و تخلیه این تراز برای ایجاد وارونی جمعیت قابل ملاحظه کفایت نمی‌کند. باید تراز بالا را نیز جمعیت‌دار کرد.


• دمش در لیزرهای الکترون آزاد
  عملکرد این لیزرها بطور بنیادین با سایر لیزرها متفاوت است. محیط تابش‌کننده الکترون‌های آزاد هستند. یعنی الکترون‌هایی که مقید به هیچ ساختار اتمی یا مولکولی نیستند. از آنجایی که ذرات باردار اگر شتاب بگیرند تابش خواهند کرد، می‌توان با شتاب دادن الکترون‌ها، از آن‌ها به عنوان منبع نور استفاده کرد. نور خروجی، بسیاری از ویژگی‌های نور لیزری را خواهد داشت. الکترون‌های آزاد ترازهای انرژی گسسته ندارند و تقریباً بطور پیوسته می‌توان انرژی آنها را تغییر داد. بنابراین در اینجا نیاز به وارونی جمعیت نیست و تنها باید به نحوی مناسب به الکترون‌ها انرژی تزریق کرد. تزریق انرژی می‌تواند از طریق میدان‌های مغناطیسی یا الکتریکی باشد. با افزایش انرژی سرعت الکترون‌ها افزایش می‌یابد. لازم است تا الکترونها بدفعات یک مسیر بسته را طی کرده و در هر بار طی مسیر انرژی بیشتری کسب کنند. تابش نور این نوع لیزرها، تابشی سینکروترونی است. برای اخذ تابش از ساختارهای مغناطیسی خاص موسوم به «موج‌زن» استفاده می‌شود. لیزرهای الکترون آزاد بدلیل قابلیت تنظیم طول موج و ویژگی‌های خوب پرتو مورد توجه بسیار هستند و در حوزه‌های تحقیقاتی علمی کاربردهای متعددی دارند.

هر یک از روش‌های دمش ذکر شده، پیاده‌سازی‌های متعددی دارند. هر منبع لیزری با توجه به ویژگی‌های خود از روشی مناسب برای دمش استفاده می‌کند. در اینجا کلیّات روش‌های دمش به عنوان آشنایی و بصورت توصیفی مطرح شد. جزئیات هر روش و نیز نحوهٔ عملکرد هر یک از مثال‌های ذکر شده باید در بحث منابع نور لیزری بطور جداگانه مطرح شود.

دینامیک ترازهای لیزری

در بحث وارونی جمعیت یک سیستم «دوترازه» در نظر گرفته شد. در این سیستم گذارهای تابشی بین تراز پایین (که ممکن است همان تراز پایه مولکول باشد) و تراز با انرژی بالاتر رخ می‌داد. دمش انرژی جمعیت تراز بالا را افزایش و فرآیندهای گسیل خودبخود و گسیل برانگیخته جمعیت آن را کاهش می‌داد. اما زمانی که بدلیل دمش، جمعیت تراز بالا زیاد می‌شود، شانس گسیل برانگیخته هم زیاد خواهد شد. تغییر جمعیت تراز را می‌توان با «معادلات واهلش» یا «معادلات آهنگ» نشان داد. میزان تغییر در جمعیت متناسب با خود جمعیت آن تراز است یعنی: \[\frac{dN_i}{dt}\propto N_i\] ضریب تناسب احتمال تغییر در جمعیت را بدلیل آن فرآیند مشخص می‌کند. اگر چند فرآیند دخیل باشند چند جمله خواهیم داشت. مثلاً در مورد تراز بالا، جمله‌ای که فرآیند جذب را نشان می‌دهد با ضریب جذب بصورت مثبت ظاهر خواهد شد و جملات مربوط به فرآیندهای گسیل برانگیخته و گسیل خودبخود بصورت منفی و با ضرایب مربوطه ظاهر می‌شوند.

در مورد یک سیستم دو ترازه، اگر \(N\) اتم داشته باشیم، این اتم‌ها بین دو تراز با انرژی \(E_1\) و \(E_2\) توزیع شده‌اند. جمعیت هر یک را بترتیب با \(N_1\) و \(N_2\) نشان میدهیم. طبیعی است که در این سیستم \(N_1+N_2=N\). اگر شروع به دمش کنیم، جمعیت ترازها شروع به تغییر خواهد کرد. برای بدست‌آوردن \(N_1(t)\) و \(N_2(t)\) از معادلات واهلش استفاده می‌کنیم. تغییرات جمعیت تراز بالا \(N_2\) ناشی از عوامل زیر است:

• افزایش جمعیت ناشی از فرآیند جذب و انتقال اتم‌ها از تراز پایین به بالا که بصورت \(W_{12}N_1\) نوشته می‌شود. \( W_{12} \) ضریب احتمال جذب است. طبیعی است که هرچه \(N_1\) بزرگتر باشد، تعداد اتم‌هایی که نور را جذب می‌کنند و به تراز بالا می‌روند بیشتر است.


• کاهش جمعیت ناشی از فرآیند گسیل برانگیخته و انتقال اتم‌ها از تراز بالا به پایین که بصورت \(W_{21}N_2\) نوشته می شود. \(W_{21}\) ضریب احتمال گسیل برانگیخته است. طبیعی است که هر چه \(N_2\) بزرگ‌تر باشد، تعداد اتم‌هایی که گسیل برانگیخته دارند بیشتر است. چون احتمال جذب و گسیل برانگیخته با هم برابر است: \(W_{12}=W_{21}\).


• کاهش جمعیت ناشی از گذارهای خودبخود از تراز بالا به تراز پایین. این گذارها را به دو دسته می‌توان تقسیم کرد: گذارهای تابشی ناشی از گسیل خودبخود (برهمکنش سیستم با خلاء کوانتومی) و گذارهای غیر تابشی ناشی از برخورد. شانس هر یک را بترتیب با \(A_{21}\) و \(S_{21}\) نشان داده و مجموع آن‌ها را با \( \gamma_{21} (=A_{21}+S_{21})\) نشان می‌دهیم. عکس این مقدار طول عمر تراز را نشان می‌دهد (\(\gamma_{12}=1/\tau_{12}\)).

در کل تغییرات جمعیت تراز بالا را می‌توان با معادلهٔ آهنگ زیر نشان داد: \[ \frac{dN_2}{dt}=W_{12}N_1-W_{21}N_2- \gamma_{21}N_2=W_{12}(N_1-N_2)-\gamma_{21}N_2 \] به همین ترتیب برای تراز پایین می‌توان نوشت: \[ \frac{dN_1}{dt}=-W_{12}(N_1-N_2)+\gamma_{21}N_2 \] دیده می‌شود که \(\frac{dN_1}{dt}+\frac{dN_2}{dt}=0\)، یعنی \( \frac{d(N_1+N_2)}{dt}=0 \) که بیان منطقی آن است که تعداد کل مولکول‌ها ثابت مانده است: \( N_1+N_2=N\).

در حالت پایا تغییرات صفر است و خواهیم داشت: \[ \frac{dN_1}{dt}=\frac{dN_2}{dt}=0\] از اینجا می‌توان نسبت جمعیت دو تراز را در حالت پایا بدست آورد: \[ \frac{N_2}{N_1}=\frac{W_{12}}{W_{12}+\gamma_{21}} \] اختلاف جمعیت نسبی بین دو تراز هم برابر است با: \[ \frac{\Delta N}{N}=\frac{N_2-N_1}{N_2+N_1}=-\frac{1}{1+2W_{12}/\gamma_{21}} \] روابط بالا نشان می‌دهد که \(N_2\) هیچگاه نمی‌تواند از \( N_1 \) بیشتر شود. این در‌واقع بیان همان مطلبی است که اشاره کردیم در یک سیستم دو ترازه به کمک دمش نوری، نمی‌توان وارونی جمعیت پایدار بوجود آورد. برای ایجاد وارونی جمعیت باید ترازهای بیشتری را دخیل کرد. بر این اساس الگوهای لیزرهای سه‌ترازه و چهار ترازه حاصل می‌شود.

لیزرهای سه‌ترازه

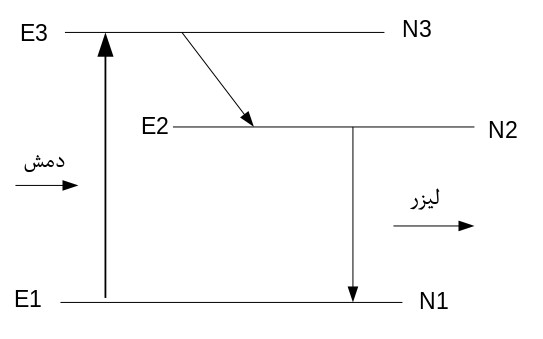در یک لیزر سه‌ترازه، سه تراز \(E_1\)، \(E_2\) و \(E_3\) با جمعیت‌های \(N_1\)، \(N_2\) و \(N_3\) در نظر گرفته می‌شود. دمش، مولکول‌ها را از تراز ۱ به تراز ۳ انتقال می‌دهد. این مولکول‌ها از طریق گذارهای عمدتاً غیرتابشی به تراز ۲ وامی‌پاشند. طول عمر این گذارها بسیار کوتاه است. تراز دوم به عنوان تراز لیزری بالا و تراز اول به عنوان تراز لیزری پایین در نظر گرفته می‌شود. به تراز سوم اصطلاحاً تراز دمش گفته می‌شود. دمش مولکول‌ها به تراز ۳ و خالی شدن سریع آن به تراز ۲ از طریق گذارهای حرارتی غیر تابشی سریع، امکان ایجاد وارونی جمعیت بین دو تراز لیزری پایین و بالا را ممکن می‌سازد. دقت کنید که چون تراز سوم سریعاً تخلیه می‌شود، امکان دمش مؤثر به این تراز وجود دارد که جمعیت تراز پایین را کاهش می‌دهد. از طرفی تراز دوم بصورت غیر مستقیم پر می‌شود. این ترکیب هوشمندانه در شکل مقابل به تصویر کشیده شده است.

طبیعتاً در اینجا انرژی دمش (\(h\nu_p\)) بیش از اختلاف انرژی بین دو تراز خواهد بود.

اگر گذارها را به همین سه تراز محدود کنیم، خواهیم داشت: \( N_1+N_2+N_3=N\). معادلات آهنگ را نیز به صورت زیر می‌توان نوشت: \[ \frac{dN_3}{dt}=W_p(N_1-N_3)-\gamma_{32}N_3 \] در این معادله، \(W_p \) آهنگ دمش از تراز ۱ به ۳ را نشان می‌دهد. جملهٔ اول بیانگر گذارهای برانگیخته بین دو تراز (یعنی جذب و گسیل برانگیخته) و جملهٔ دوم گذار خودبخود بین ترازهای ۲ و۳ را نشان می‌دهد. این جمله هم شامل گذارهای تابشی با آهنگ وقوع \(A_{32} \) و هم گذارهای غیر تابشی با آهنگ \(S_{32} \) است. در اینجا از گذار خودبخود بین تراز ۳ و ۱ صرفنظر شده است چون فرض بر این است که واپاشی به تراز دوم بسیار سریع است و اغلب مولکول‌هایی که به تراز ۳ رفته‌اند به تراز ۲ وامی‌پاشند.

معادلات آهنگ برای دو تراز دیگر هم به شکل مشابهی نوشته می‌شوند: \[ \frac{dN_2}{dt}=-W_1(N_1-N_2)+\gamma_{32}N_3-\gamma_{21}N_2 \] \[ \frac{dN_1}{dt}=W_p(N_3-N_1)+W_1(N_2-N_1)+\gamma_{21}N_2 \] در حالت پایا خواهیم داشت: \( \frac{dN_1}{dt}=\frac{dN_2}{dt}=\frac{dN_3}{dt}=0 \). جمعیت ترازهای بالا نسبت به تراز اول را هم می‌توان از معادلات بالا بدست آورد: \[ \frac{N_3}{N_1}=\frac{W_p}{W_p+\gamma_{32}} \] \[ \frac{N_2}{N_1}=\frac{W_1(\gamma_{32}+W_p)+W_p\gamma_{32}}{(W_p+\gamma_{32})(W_1+\gamma_{21})} \] و اختلاف جمعیت نسبی بین دو تراز لیزری برابر خواهد شد با: \[ \frac{N_2-N_1}{N}=\frac{W_p(\gamma_{32}-\gamma_{21})-\gamma_{32}\gamma_{21} }{3W_pW_1+2W_p\gamma_{21}+2W_1\gamma_{32}+W_p\gamma_{32}+\gamma_{32}\gamma_{21}} \] بر این اساس برای داشتن وارونی جمعیت (یعنی مثبت بودن عبارت \( N_2-N_1 \) )لازم است دو شرط زیر برقرار شود:

1. \( \gamma_{32}>\gamma_{21} \) باشد، یعنی \( \tau_{21} > \tau_{32} \). به عبارت دیگر طول عمر تراز ۳ کوچکتر از طول عمر تراز ۲ باشد.


2. با آهنگ مناسبی مولکول‌ها به تراز ۳ دمیده شوند. میزان دمش باید بیشتر از مقدار حداقل \( \frac{\gamma_{32}\gamma_{21}}{\gamma_{32}-\gamma_{21}} \) شود.

لیزرهای چهارترازه

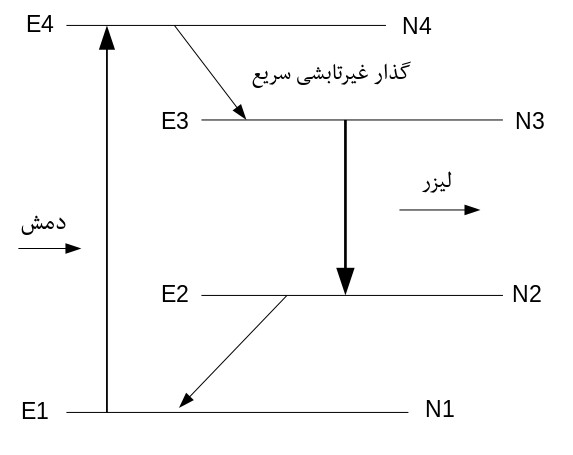طبیعی است که برای ایجاد وارونی جمعیت بین دو تراز ۱ و ۲ باید حداقل نیمی از مولکول‌های تراز پایه را انتقال داد. اگر بخواهیم از این محدودیت فرار کنیم می‌توان تراز لیزری پایین را همان تراز پایه نگرفت همانطور که بین تراز بالای لیزری و تراز پمپ تفاوت قائل شدیم. این امر منجر به ایجاد یک لیزر چهارترازه خواهد شد که در شکل مقابل دیده می‌شود. مولکول‌ها از تراز ۱ به تراز ۴ دمیده می‌شوند. مولکول‌های تراز ۴ با گذارهای غیرتابشی به تراز ۳ وامی‌پاشند. تراز ۳ که به مثابهٔ تراز بالایی لیزر عمل می‌کند، شبه پایدار است، یعنی طول عمر زیادی دارد. تراز ۲، تراز پایینی لیزر خواهد بود و گذار لیزری بین تراز ۳ و ۲ اتفاق می‌افتد. از طرفی تراز ۲ طول عمر بسیار کوتاهی دارد و مولکول‌های آن سریعاً به تراز ۱ می‌روند. در نتیجه تراز بالایی لیزر (تراز سوم) از طریق تراز ۴ مرتباً جمعیت‌دار می‌شود و بخاطر طول عمر زیاد جمعیت خود را حفظ می‌کند. امّا تراز پایینی لیزر (تراز دوم) بدلیل طول عمر پایین مرتباً جمعیت خود را از دست می‌دهد. این امر منجر به وارونی جمعیت بین دو تراز ۲ و ۳ خواهد شد. دقت کنید که نیازی نیست عمل دمش بین ترازهای ۱ و ۴، وارونی جمعیت بوجود آورد و به همین خاطر توان دمش کوچکتر هم می‌تواند کفایت کند.

از طرفی انرژی تراز دوم نباید خیلی به انرژی تراز اول نزدیک باشد، چون در این حالت بدلیل توزیع بولتزمان جمعیت قابل ملاحظه‌ای در آن خواهند بود که وارونی جمعیت را کاهش خواهد داد. البته می‌توان با کاهش دمای محیط این مشکل را تا حد زیادی برطرف کرد.

نکتهٔ دیگر آنکه در بسیاری از موارد عملی، تراز چهارم لازم نیست یک تراز با انرژی مشخص باشد، بلکه می‌تواند یک نوار انرژی متشکل از تعداد زیادی تراز نزدیک به هم باشد که همگی به تراز ۳ وامی‌پاشند. این امر باعث می‌شود که بتوان برای دمش نوری از یک منبع با طیف نسبتاً پهن هم استفاده کرد و در‌ واقع بهرهٔ دمش را بالا برد.

معادلات آهنگ را برای این سیستم چهار ترازه مشابه قبل بصورت زیر می‌توان نوشت: \[ \frac{dN_4}{dt}=W_p(N_1-N_4)-\gamma_{43}N_4 \] \[ \frac{dN_3}{dt}=W_1(N_2-N_3)+\gamma_{43}N_4-\gamma_{32}N_3 \] \[ \frac{dN_2}{dt}=-W_1(N_2-N_3)+\gamma_{32}N_3-\gamma_{21}N_2 \] \[ \frac{dN_1}{dt}=-W_p(N_1-N_4)+\gamma_{21}N_2 \] اگر فرض کنیم تمام مولکول‌ها در این چهار تراز توزیع شده‌اند، خواهیم داشت: \[ N_1+N_2+N_3+N_4=N \] در حالت پایا خواهیم داشت: \[ \frac{dN_1}{dt}=\frac{dN_2}{dt}=\frac{dN_3}{dt}=\frac{dN_4}{dt}=0 \] در این وضعیت نسبت جمعیت تراز چهارم به تراز پایه برابر خواهد بود با: \[ \frac{N_4}{N_1}=\frac{W_P}{W_P+\gamma_{43}} \] اگر واهلش از تراز ۴ به ۳ خیلی سریع باشد، \( \gamma_{43} \) خیلی کوچکتر از \(W_p\) است و بنا بر این \( N_4\ll N_1 \) می‌شود. با این فرض اختلاف نسبی جمعیت دو تراز لیزری را می‌توان بدست آورد: \[ \frac{N_3-N_2}{N}\approx \frac{W_p(\gamma_{21}-\gamma_{32})}{W_p(\gamma_{21}+\gamma_{32})+\gamma_{32}\gamma_{21}+W_1(2W_p+\gamma_{21})} \] این رابطه نشان می‌دهد که برای داشتن وارونی جمعیت بین دو تراز لیزری ۲ و۳ باید آهنگ انتقال مولکول‌ها از تراز ۲ به تراز ۱ بیشتر از آهنگ انتقال از تراز ۳ به تراز ۲ باشد. شرطی که قبلاً راجع به آن صحبت شد. دیده می‌شود که در اینجا در صورت برقراری این شرط، حتی با مقدار دمش کوچکی هم می‌توان به وارونی جمعیت رسید و مثل حالت سه‌ترازه مقدار حداقلی نیاز نیست.

در صورتی که اختلاف آهنگ‌های انتقال خیلی زیاد باشد (یعنی \( \gamma_{21}\gg \gamma_{32} \) ) رابطه وارونی جمعیت بصورت زیر درمی‌آید: \[ \frac{N_3-N_2}{N}\approx \frac{W_p}{W_p+\gamma_{32}} \times \frac{1}{1+W_1(\gamma_{21}+2W_P)/\gamma_{21}(W_p+\gamma_{32})} \] وارونی جمعیت بصورت حاصلضرب دو جمله بیان شده است.جمله اول فقط به توان دمش (\(W_p\)) ربط دارد و حالتی را نشان می‌دهد که توان لیزری (\(W_1\)) از سیستم اخذ نشود. این عبارت حالت تقویت‌کنندگی محیط را نشان می‌دهد و در‌ واقع همان بهرهٔ سیگنال کوچک سیستم است. نمونهٔ بارز منابع لیزری که با الگوی چهارترازه کار می‌کنند، لیزر Nd:YAG است.

نکات پایانی

• در بسیاری از لیزرهای عملی، ترازهای مورد استفاده در محیط فعال فقط یک تراز انرژی ثابت نیست، بلکه از مجموعه‌ای تراز نزدیک به هم تشکیل می‌شود که بیشتر بصورت یک باند یا نوار انرژی است. این امر هم در مورد ترازهای پمپ و هم در مورد ترازهای لیزری صدق می‌کند. مورد اخیر می‌تواند به نوعی پهن شدگی طیف تابشی منجر شود.


• در یک محیط فعال لیزری ممکن است چندین خط لیزری با هم فعال شوند. میزان انرژی وارد شده به هر تراز و وارونی جمعیت ایجاد شده برای آنها و نیز بهره محیط بازای هر طول‌موج متفاوت است. معمولاً سعی می‌شود از فعال شدن همهٔ این خطوط جلوگیری شود تا انرژی پخش نشود و کارآیی سیستم در طول موج انتخاب شده افزایش یابد. به عنوان نمونه می‌توان از لیزر هلیوم-نئون یاد کرد که در طول موج اصلی ۶۳۲.۸ نانومتر تابش می‌کند اما همزمان در طیفی از خطوط مادون قرمز، زرد، نارنجی و سبز نیز تابش دارد. برای رسیدن به این طول موج‌ها حفره به نحوی طراحی می‌شود که طول موج مورد نظر را ارجحیت دهد (مثلاً با پوشش مناسب روی آینه‌ها برای طول موج دلخواه و یا افزودن ترکیباتی به محیط که در طول موج‌های غالب ناخواسته جاذب هستند.).


• ترازهای دخیل در تولید نور لیزری لازم نیست همگی مربوط به یک مولکول باشند. می‌توان مخلوطی از مولکول‌ها را داشت که با همدیگر در اثر برخورد یا مکانیزم‌های دیگر تبادل انرژی دارند. به عنوان مثال در لیزر هلیوم-نئون، تراز دمش در مولکول هلیوم و ترازهای لیزری مربوط به نئون است. ترازهای برانگیختهٔ هلیوم، بسیار نزدیک به برخی از ترازهای برانگیخته نئون است. مولکول‌های هلیوم در برخورد با مولکول‌های نئون آن را برانگیخته می‌کنند. این ترازهای برانگیخته می‌توانند به ترازهای پایین‌تری واهلش کنند که به نوبهٔ خود با گذارهایی بسیار سریع به حالت پایه بر می‌گردند. بنابراین عموماً محیط لیزری، یک محیط همگن از یک مولکول نیست و مخلوطی از مولکول‌ها را در برمی‌گیرد.
  مولکول‌های دیگر نقش‌های متفاوتی را ایفا خواهند کرد که یکی از آن‌ها مشارکت در فرآیند دمش و کمک به ایجاد وارونی جمعیت است. چگالی و تعداد این مولکول‌ها ممکن است بمراتب بیش از مولکول‌های اصلی باشد. در لیزر هلیوم-نئون معمولاً این نسبت ۹ به ۱ است. در لیزر دی‌اکسید کربن نیز مخلوطی از گازهای دی‌اکسید کربن، نیتروژن و هلیوم (یا بخار آب) و گاهی مقادیری هیدروژن یا زنون استفاده می‌شود. در مورد لیزرهای حالت جامد، محیط معمولاً از یک شبکهٔ بلوری میزبان تشکیل می‌شود که یون‌های مختلف بصورت ناخالصی بسیار جزیی در آن قرار گرفته‌اند. به عنوان نمونه در لیزر یاقوت، این یون‌های \( {\rm Cr^{+3}} \) هستند که نقش محیط فعال را ایفا خواهند کرد و در شبکهٔ بلوری از میزبان \( {\rm Al_2O_3} \) قرار گرفته‌اند. در لیزر Nd:YAG، یون‌های نئودیمیوم و در لیزرهای فیبری، یون‌هایی مانند اربیوم نقش ایفا می‌کنند.


• ترکیب چندترازه دیگری که می‌توان داشت، وضعیتی است که در آن دمش مستقیماً به تراز لیزری بالا انجام می‌شود، اما تراز لیزری پایین همان تراز پایه نیست و مولکل‌ها از تراز پایینی به تراز پایه واهلش سریع دارند که منجر به ایجاد وارونی جمعیت می‌شود. این ساختار الگویی سه‌ترازه است اما چون عملکرد تراز پایین شبیه لیزرهای چهارترازه است، گاهی از آن به عنوان لیزر چهارترازه نیز یاد می‌شود. یکی از امتیازهای چنین سیستمی این است که در آن اُفت انرژی مربوط به گذار از تراز دمش به تراز بالا حذف می‌شود و راندمان بالاتری خواهد داشت.

این مبحث ادامه دارد و تکمیل خواهد شد.