معرفی مولکول

یکی از مهمترین برهمکنش‌های موجود در عالم در قالب «برهمکنش الکترومغناطیسی» توصیف می شود. اهمیت این برهمکنش در طیف وسیع پدیده‌هایی است که در بر می‌گیرد. تقریباً عمدهٔ فرآیندهایی که بطور روزمره با آنها مواجه هستیم، در این چارچوب می‌گنجند. نظریهٔ مکانیک کوانتومی را می‌توان برای سیستم‌هایی که در آنها این برهمکنش غالب است، بکار گرفت. به این سیستم‌ها «مولکول» می‌گوییم.

ذراتی با هم برهمکنش الکتریکی دارند که دارای ویژگی مشترک «بار الکتریکی» باشند. الکترون‌ها و پروتون‌ها با بارهای منفی و مثبت خود عمدهٔ بازیگران هستند. بنابراین مولکول‌ها سیستم‌هایی متشکل از پروتون و الکترون هستند. البته این به معنای عدم وجود سایر ذرات در این سیستم‌ها نیست. ذراتی فاقد بار الکتریکی نیز در آنها موجود است که برهمکنش‌هایی از نوع دیگر دارند. این ذرات بر شکل نهایی سیستم اثر می‌گذارند. امّا در مولکول‌ها، آنچه تعیین کننده «حالت» است، برهمکنش الکترومغناطیس است. سایر برهمکنش‌ها، بیشتر «ساختار» را تعیین می‌کنند. ساختار اگر چه نوع حالت‌های ممکنه را مشخص می‌کند، امّا عموماً در تحول حالت سیستم ثابت می‌ماند.

برای فهم بیشتر مولکول به این مثال دقت کنید.
فرض کنید چهار ذره داریم: دو الکترون و دو پروتون. چه سیستم‌های پایداری با آنها شکل می‌گیرند؟ به چند نمونه توجه کنید:

• هر چهار ذره تقریباً بصورت ذرات آزاد باشند و برهمکنش الکتریکی ناچیزی با هم داشته باشند، به شکل یک گاز. انرژی تک تک ذرات کمابیش می‌تواند هر مقدار پیوسته‌ای بخود بگیرد. انرژی کل سیستم مجموع این انرژی‌ها خواهد بود. و حالات نسبتاً پیوسته‌ای خواهیم داشت.


• یک الکترون با یک پروتون برهمکنش شدید داشته باشد و الکترون و پروتون دیگر آزاد باشند. الکترون و پروتون اول، آزادی عمل خود را از دست می‌دهند و حالت نهایی آنها بر اساس میزان برهمکنش‌شان باید تعیین شود. در‌ واقع در این وضعیت، این دو ذرّه یک سیستم کوچکتر یا زیر سیستم تشکیل داده‌اند که اصطلاحاً به آن «اتم هیدروژن» H می‌گوییم.


• دو اتم هیدروژن شکل بگیرد امّا آن دو مستقل از هم عمل کنند. یعنی بین این دو سیستم کوچک برهمکنشی نداشته باشیم. گاز هیدروژنی متشکل از دو اتم هیدروژن داریم (2H).


• دو اتم هیدروژن شکل بگیرد ولی آنقدر به هم نزدیک باشند که برهمکنش الکترومغناطیسی قابل ملاحظه‌ای بین آن دو باشد. به نحوی که ذرات مستقل از هم عمل نمی‌کنند. مولکول هیدروژن (H2) ساخته خواهد شد.


• دو پروتون به هم نزدیک شده و در کنار هم قرار بگیرند. این کار در چارچوب برهمکنش الکترومغناطیس ناممکن است. چون نیروی بین دو پروتون دافعه است. امّا اگر به یاد بیاوریم که پروتون‌ها نوعی بار برهمکنش دیگر هم دارند که در قالب برهمکنش هسته‌ای خود را نشان می‌دهد و حالت جاذبه دارد و قوی امّا کوتاه بُرد است، می‌توان تصور کرد که دو پروتون با چنان سرعتی به هم برخورد کرده‌اند که بر نیروی دافعه الکترومغناطیس غلبه کرده و توانسته‌اند آنقدر به هم نزدیک شوند که نیروی جاذبهٔ هسته‌ای آنها را در کنار یکدیگر قرار دهد و یک سیستم تشکیل دهند. البته در اینجا برای افزایش برهمکنش هسته‌ای و پایدار بودن آن، یک یا دو ذره بدون بار الکتریکی ولی دارای بار هسته‌ای (موسوم به نوترون) به این مجموعه اضافه می‌شود. همانطور که سیستم‌های شکل‌گرفته بر اثر برهمکنش الکتریکی را مولکول نامیدیم، به این سیستم‌ها «هسته» می‌گوییم. دو الکترون می‌توانند با این بار مثبت کُلّی برهمکنش کرده و سیستم نهایی را ایجاد کنند. در واقع در اینجا یک زیرسیستم «هسته» داریم که با دو الکترون یک مولکول می سازند: مولکول موسوم به «اتم هلیوم» He.


• یک هستهٔ هلیوم شکل بگیرد و یک الکترون در دام آن بیفتد، اما الکترون دیگر آزاد باشد.در اینجا با «یون هلیوم» مواجه هستیم و یک الکترون کمابیش آزاد. لفظ «یون» عموماً زمانی بکار می‌رود که مجموع بار الکتریکی آن سیستم صفر نباشد.

همانگونه که دیده‌ می‌شود، با ترکیب چهار ذرهٔ باردار به ساختارهای متعددی رسیدیم. ساختارهای ذکرشده پایا بودند یعنی ساختارهایی پایدار و با ثبات. ترکیبات دیگری هم می‌توان در نظر گرفت که دوام چندانی ندارند و سریع به یکی از حالات پایا واهلش پیدا می‌کنند. با افزایش تعداد ذرات به ساختارهای پیچیده‌تری هم دست پیدا می‌کنیم که بر اساس آن انواع مولکول‌ها و اتم‌های متعارف بدست می‌آیند.

هر یک از ساختارهای پایا، می‌توانند در حالات کوانتومی مشخصی قرار گیرند. هر یک از این حالت‌ها، انرژی مشخصی خواهد داشت. مشابه همهٔ سیستم‌های کوانتومی، همهٔ حالات انرژی پایا نیستند (یعنی ویژه حالت انرژی نیستند). در بررسی سیستم، مهم بدست‌ آوردن حالات پایای آن است. به این حالت‌ها ترازهای انرژی هم گفته می‌شود. سیستم می‌تواند با داشتن انرژی مشخص، در یکی از این حالات باشد و تا زمانی که اختلال یا برهمکنشی با آن رخ ندهد در همان حالت باقی خواهد ماند. محدودهٔ انرژی سیستم‌هایی شبیه اتم هیدروژن و مولکول هلیوم در حد چند الکترون ولت یا چند ده الکترون ولت است و برای ساختارهای پیچیده با تعداد ذرات بیشتر ممکن است به صدها الکترون ولت برسد.

در اتمی مثل هلیوم، وابستگی دو الکترون به هسته یکسان نیست. بنابراین اگر بخواهیم از ساختار اتم هلیوم به یون هلیوم برسیم و برای اینکار به آن انرژی بدهیم، ابتدا الکترونی که وابستگی کمتری دارد آزاد خواهد شد. به انرژی لازم برای اینکار، انرژی «تشکیل یون» یا «یونیزاسیون» می‌گویند. با افزایش تزریق انرژی، الکترون دوم هم ممکن است آزاد شده و هسته آن تنها بماند (یون \({\rm He}^{+2}\) ). به این الکترون دوم اصطلاحاً الکترون داخلی می‌گویند و به الکترون اول الکترون بیرونی. این اصطلاح در مورد مولکول‌های با تعداد الکترون بیشتر هم بکار می‌رود. این اصطلاحات ممکن است این مسئله را القاء کند که هر چه انرژی حالتی بیشتر باشد، بیشینهٔ توزیع فضایی الکترون (یعنی جایی که شانس پیدا کردن آن حداکثر می‌شود) به هسته نزدیکتر است. اما این امر لزوماً درست نیست. بعضی از حالات، انرژی بالاتری دارند امّا توزیع فضایی دورتری از هسته. علاوه بر این بسیار اتفاق می‌افتد که یک توزیع فضایی چندین بیشینه دارد.

چند نکته در رابطه با اسامی:
هنگام صحبت در بارهٔ مولکول‌ها، گاهی از لفظ اتم استفاده می‌شود. معمولاً این لفظ برای سیستم‌هایی استفاده می‌شود که یک زیرسیستم هسته دارند. لفظ مولکول هم به ساختارهای با چند هسته اطلاق می‌شود. به همین خاطر است که در مثال‌های بالا می‌گوییم اتم هلیوم ولی مولکول هیدروژن. اما دقت داشته باشید که لفظ عمومی‌تر همان «مولکول» است که به همه سیستم‌های با برهمکنش الکترومغناطیس از جمله اتم‌ها و یون‌ها نسبت داده می شود. لفظ «هسته» هم به همهٔ ساختارهایی اطلاق می‌شود که در آنها ذرات با هم برهمکنش هسته‌ای دارند. در این هسته‌ها ممکن است ذراتی که بار الکتریکی ندارند اما بار هسته‌ای دارند (نظیر ذرهٔ نوترون) نیز حضور داشته باشند.

«فیزیک اتمی و ملکولی» یا بطور خلاصه «فیزیک مولکولی» به سیستم‌های نوع اول یعنی مولکول‌ها می‌پردازد و ساختار و حالات انرژی آنها را مطالعه می‌کند. «فیزیک هسته‌ای» سیستم‌های نوع دوم را بررسی می‌کند و ساختار و حالات انرژی آنها را بدست می‌آورد. انرژی حالات گروه اول از چند صد الکترون ولت تجاوز نمی‌کند. اما حداقل انرژی سیستم‌های هسته‌ای از ردهٔ مگا الکترون ولت است. بنابراین بطور ساده می‌توان گفت: فیزیک اتمی و مولکولی یعنی فیزیک انرژی‌های زیر پانصد الکترون ولت. به همین ترتیب گاهی از فیزیک هسته‌ای با لفظ «فیزیک انرژی زیاد» نیز یاد می شود.

در محدودهٔ فیزیک اتمی و مولکولی، با توجه به اختلاف زیاد بین انرژی‌های این دو برهمکنش، از انرژی هسته صرفنظر می‌شود. چون اگر چه مقدار انرژی بزرگ است اما در تحولات مولکولی همواره مقدار آن ثابت است.

رفتار جمعی مولکول‌ها

اگر تعداد زیادی مولکول مشابه داشته باشیم، رفتار جمعی آنها نیز اهمیت پیدا می‌کند. در عمل در اکثریت قریب به اتفاق موارد با مجموعه‌های آماری بسیار بزرگ از مولکول‌ها مواجه هستیم. در حالتی که برهمکنش بین تک تک مولکول‌ها کم باشد، با گازی از آنها روبرو خواهیم بود. رفتار سیستم از برخوردها و مواجهه‌های گاه به گاه این مولکول‌ها تأثیر می‌پذیرد. در حالت‌هایی که برهمکنش شدید می‌شود، مولکول‌ها بسیار محدود شده و مجبورند علاوه بر حفظ موازنه انرژی درونی، برهمکنش شدید با مولکول‌های مجاور را نیز ساماندهی کنند. گاهی حل این مسئله منجر به تثبیت موقعیت هر مولکول در محدودهٔ مشخصی از فضا می‌شود و شبکه‌ای از نقاط فضا را داریم که مولکول‌ها تنها در آن نقاط قرار می‌گیرند. به این نقاط اصطلاحاً «شبکهٔ بلوری» می‌گویند. علاوه بر این ممکن است بعضی از الکترون‌هایی که وابستگی کمتری به هستهٔ خود دارند (الکترون‌های لایه‌های بیرونی) عملاً با جابجا شدن بین حوزهٔ اثر هسته‌های مختلف تقریباً آزادانه حرکت کنند. مانند آن است که هر مولکول‌، بخشی از اجزای خود را به اشتراک گذارده و هویتی جمعی بوجود آمده است. این موضوع منجر به ایجاد تعداد بسیار زیادی از حالت‌های انرژی نزدیک به هم می‌شود که ممکن است محدودهٔ پیوسته‌ای از ترازهای انرژی موسوم به «نوارهای انرژی» را بوجود آورند.

در وضعیتی دیگر، امکان دارد یک مولکول خاص بتواند ترکیبی پایدار با مولکولی مشابه خود را ایجاد کند یعنی اصطلاحاً با هم پیوند برقرار کنند. برحسب میزان انرژی و پایداری این پیوند، آنها را به دسته‌های مختلفی تقسیم می‌کنند. در شرایطی این پیوند بین مولکول‌های مشابه می‌تواند به کرّات تکرار شود و یک ساختار بسیار بزرگ متشکل از چند هزار تا چند صد هزار ذره را بسازد. به این ساختارها «پلیمر» می‌گویند و به هر جزء تکرار شونده آن یک «مونومر». نام کُلّی «ماکرومولکول» نیز به این ساختارها اطلاق می‌شود.

در حالت عام‌تر ممکن است بین بخش‌های مختلف یک پلیمر نیز پیوندهایی برقرار شود که پایدار باشند و باعث آرایش خاص فضایی ماکرومولکول شود. در این حالت که بتدریج مولکول‌ها بزرگ‌تر و بزرگ‌تر می‌شوند، کم کم مفهوم شکل و ریخت در بارهٔ ماکرومولکول صدق خواهد کرد و شاهد برخی رفتارهای ماکروسکوپی از مولکول خواهیم بود که با مفاهیم مکانیک کلاسیک سازگارتر است تا مفاهیم مکانیک کوانتومی. اگر چه سیستم ویژگی‌های کوانتومی خود را حفظ می‌کند. این سیستم‌ها را اصطلاحاً سیستم‌های مزوسکوپی (یا نانو سیستم) می‌نامند.

اتم هیدروژن: ساده‌ترین مولکول

ساده‌ترین ساختار مولکولی شامل یک الکترون و یک پروتون است که با هم برهمکنش الکترومغناطیسی قابل ملاحظه‌ای داشته باشند، یعنی اتم هیدروژن.

توصیف کیفی اتم هیدروژن

ابتدا سعی می‌کنیم با در نظر گرفتن ویژگی‌های برهمکنش ببینیم چه اطلاعات کیفی راجع به حالات ممکنه سیستم می‌توان پیدا کرد. مهمترین ویژگی این برهمکنش تقارن فضایی آن است. با توجه به نقطه‌ای در نظر گرفتن الکترون و پروتون، برهمکنش بین آن دو، تقارن زاویه‌ای (تقارن کروی) دارد. به عبارت دیگر میزان نیرو تنها به فاصلهٔ بین دو ذره بستگی دارد و مستقل از جهت‌گیری در فضاست. به عبارت دیگر اگر برای مشخص کردن موقعیت نسبی ذرات از یک طول (\(r\)) و دو زاویه (\(\theta\) و \(\phi\)) استفاده کنیم، نیرو فقط به \(r\) بستگی خواهد داشت.

اگر بیان فضایی حالت کوانتومی سیستم را تنها بصورت تابع توزیع فضایی الکترون در نظر بگیریم (چون پروتون سنگین‌تر است و می‌توان توزیع فضایی آن را در محدودهٔ تحولات مولکولی ثابت در نظر گرفت)، تابع توزیع سیستم بصورت \(\psi(\vec r, t)=\psi(r,t)\) خواهد بود و هیچ وابستگی زاویه‌ای نخواهد داشت. چه توزیع‌هایی این ویژگی را خواهند داشت؟ هر توزیع کروی یک کاندید خواهد بود. بنابراین در ساده‌ترین حالت می‌توان یک توزیع متقارن کروی را در نظر گرفت که در کل فضا پخش شده است و در جایی احتمال آن حداکثر خواهد بود.

با توجه به اینکه اندازهٔ بردار حالت \(\psi(r,t)\)، احتمال یافتن ذره را نشان می‌دهد، می‌توان گفت که الکترون در هر ناحیه‌ای از فضا اطراف هسته می‌تواند باشد. البته ما بدنبال ساختارهای پایا یا تشدیدی هستیم. بنابراین توزیع‌هایی پایا خواهند بود که در نقاط مشخصی از فضا بیشینه داشته باشند. مقدار شعاع بیشینه را می‌توان به عنوان عدد کوانتومی سیستم در نظر گرفت. امّا با توجه به اهمیت کمیّت انرژی به عنوان عدد کوانتومی اصلی سیستم می‌توان انرژی مرتبط با هر یک از این شعاع‌ها را به عنوان توصیف سیستم در نظر گرفت. اگر شعاع‌های بیشینه را به ترتیب با \(r_1, r_2, r_3, \cdots\) نشان دهیم، انرژی‌های آنها \(E_1, E_2, E_3, \cdots\) است و حالات متناظر را می‌توان با اندیس آنها مشخص کرد: \(|1>, |2>, |3>, \cdots\) . یعنی در حالت کلی سیستم با \(|n>\) مشخص می‌شود (دلیل گسسته در نظر گرفتن حالات می‌تواند اتکاء به نتایج تجربی یا ملاحظات نظری مرتبط به حالات تشدیدی باشد.). پذیرفتنی است که اگر فقط توزیع‌های کروی را در نظر بگیریم، هر چه شعاع بیشینه دورتر از هسته باشد، انرژی سیستم کمتر خواهد بود. در صورتی که فاصلهٔ بسیار دور از الکترون را به عنوان مبدأ سنجش انرژی (انرژی صفر) انتخاب کنیم، همهٔ انرژی‌های سیستم منفی خواهند بود که الکترونی مقید را نشان می‌دهد.

بنظر می‌رسد که توانستیم با تکیه بر تقارن برهمکنش، با یک عدد کوانتومی اتم هیدروژن را توصیف کنیم. اما بایستی مراقب بود. فقط توزیع‌های کروی لایه‌ای نیستند که تقارن کروی دارند! می‌توان توزیع‌های فضایی در نظر گرفت که به تنهایی تقارن کروی ندارند امّا ترکیب آنها منجر به این تقارن خواهد شد. به عنوان نمونه توزیعی با تقارن حول محور x را در نظر بگیرید. این توزیع قطعاً به زاویه بستگی خواهد داشت و فاقد تقارن کروی است. شبیه همین حالت برای توزیع‌های متقارن حول محور y و z هم صادق است. امّا اگر ترکیبی هم‌وزن از این سه توزیع را داشته باشیم چه؟ هر یک از آنها بخشی از تقارن فضایی کروی را فراهم خواهند کرد و ترکیب آنها تقارن زاویه‌ای پیدا می‌کند. مانند این است که سه حالت مجزای الکترون با هم ترکیب شده‌اند و حالت ترکیبی را بوجود آورده‌اند. طبیعی است که چون محورهای x و y و z هیچ ارجحیتی با هم ندارند بنابراین انرژی این سه حالت مختلف با هم یکسان خواهند بود. به عبارت دیگر می‌توان حدس زد که صرف عدد کوانتومی n نمی‌تواند حالات مختلف را از هم تفکیک کند.

چه باید کرد؟ باید به سراغ اندازه‌گیری دیگری رفت که آنها را جدا سازد. امّا چگونه؟ این حالات که همانند بودند. از کجا می‌توان فهمید که پیدا کردن یک لایهٔ کروی در فضا با شعاع مشخص به عنوان محل بیشینهٔ حضور الکترون ناشی از توزیع متقارن کروی آن حول پروتون است، یا ترکیبی از حالات با انرژی یکسان را نشان می‌دهد. راه حل آن است که «تقارن فضا را به هم بزنیم!». به هر ترتیبی که برابری جهت‌های مختلف فضا را تغییر دهیم، رفتار این حالاتِ همانند، متفاوت خواهد شد. اعمال یک میدان الکتریکی یا مغناطیسی نامتقارن در جهت خاصی از فضا، تقارن همسانگردی فضا را می‌شکند و هر یک از این حالات سه‌گانه به نحوی متفاوت رفتار خواهد کرد. در‌واقع الکترون در اینجا غیر از برهمکنش الکترومغناطیس متقارن با پروتون، با آن میدان الکتریکی یا مغناطیسی جهتدار هم برهمکنش خواهد داشت و بسته به اینکه در کدام یک از حالت‌های متقارن نسبت به محورهای x و y و z باشد، انرژی متفاوتی پیدا خواهد کرد. اگر با اعمال میدان بیرونی و شکست تقارن فضا، تغییری در انرژی ایجاد نشد، معنای آن این است که توزیع فضایی الکترون، توزیعی کروی بوده است، ولی اگر با اعمال میدان چند انرژی مختلف را مشاهده کردیم، طبیعتاً با حالاتی از الکترون‌ها سر و کار داریم که توزیعی غیرکروی دارند.

توزیع‌های متقارن حول سه محور تنها حالاتی نیستند که ترکیب آنها توزیعی کروی را به ما می‌دهد. می‌توان مثلاً پنج توزیع متقارن نسبت به پنج محور را فرض کرد که ترکیب آنها توزیعی کروی را به ما می‌دهد و الکترون در یک فضای همسانگرد متقارن می‌تواند بین این حالات با انرژی یکسان جابجا شود، بدون آنکه عدد کوانتومی اصلی آن تغییر کند. چندین حالت متفاوت که باید آنها را با یک عدد کوانتومی دیگر مثل \(\ell\) تفکیک کرد. بنا بر این توصیف دقیق‌تر حالت اتم هیدروژن به صورت \(|n, \ell>\) خواهد بود.

در صورتی که بخواهیم شباهتی با مکانیک کلاسیک برقرار کنیم، می‌بینیم که در آنجا چیزی که یک حرکت کروی حول یک نقطه را از حرکت‌های با انرژی مشابه اما مسیرهای متفاوت تفکیک می‌کند، مفهوم «اندازه حرکت زاویه‌ای» است. بنا بر این می‌توان گفت که در حالت کوانتومی هم اندازه‌گیری دوم ما، پس از انرژی، اندازه‌گیری اندازه حرکت زاویه‌ای \(\vec L\) بوده است. طبیعی است که با هر انرژی نمی‌توان هر اندازه حرکتی داشت. بنابراین بازای هر مقدار انرژی، محدودهٔ مشخصی از اندازه‌ حرکت‌های زاویه‌ای مجاز هستند. انتظار می‌رود اندازه حرکت زاویه‌ای هم گسسته باشد.

در بحث بالا تنها اندازهٔ اندازه حرکت زاویه‌ای را در نظر گرفتیم، طبیعی است که جهت آن هم مؤثر است. بنابراین باید یک عدد کوانتومی مرتبط با جهت آن را به توصیف حالت سیستم اضافه کرد. دقت کنید که در حین اندازه‌گیری اندازه حرکت، ما تقارن فضا را در یک جهت شکستیم، امّا در انتخاب خود این جهت هم آزادی عمل وجود دارد و اندازه حرکت الکترون می‌تواند زوایای متفاوتی با آن داشته باشد. پس لازم است که جهت اندازه حرکت زاویه‌ای را هم اندازه بگیریم. به عبارت دیگر می‌توان الکترونی را فرض کرد که در حالت با انرژی \(E_i\) قرار دارد و مقدار اندازه حرکت زاویه‌ای آن هم \(L\) و در جهت خاصی از فضا است. باید بتوان حالت آن را از همین الکترون با همین انرژی و همین اندازه حرکت در جهت دیگری از فضا تفکیک کرد. چرا که این حالات از نظر انرژی و اندازه حرکت یکسانند و الکترون می‌تواند تغییر حالت بدهد بدون اینکه این کمیت‌ها تغییر کنند. پس باید برای توصیف کامل الکترون اندازه‌گیری دیگری انجام داد و جهت اندازه حرکت زاویه‌ای را بدست آورد. اعمال میدان مغناطیس جهتدار این تقارن فضایی نسبت به زاویه را بر هم خواهد زد و سیستم را نسبت به جهت حساس خواهد کرد. این کمیت اخیر عدد کوانتومی دیگری به ما می‌دهد که آن را با \(m\) نشان می‌دهیم. انتظار می‌رود که این کمیت هم تنها مقادیر گسسته‌ای را به خود بگیرد. معمولاً جهت مرجع را z می‌نامند.

بنابراین تا الان سیستم با بردار کت \(|n, \ell, m>\) و سه عدد کوانتومی حاصل از اندازه‌گیری مشخص می‌شود.

امّا، این توصیف هنوز کامل نیست. چون اسپین ذاتی الکترون را فراموش کرده‌ایم. آن را اندازه‌گیری کرده و به توصیف سیستم اضافه می‌کنیم. همانگونه که قبلاً اشاره شد اسپین به میدان مغناطیسی حساس است. بنا بر این می‌توان آن را نیز به کمک میدان خارجی اعمالی بر اتم هیدروژن اندازه‌گیری کرد.

بر اساس این توصیف کیفی، حالت اتم هیدروژن با بردار کِت زیر تعریف می‌شود: \[|n, \ell, m, s>\]

در این توصیف اعداد کوانتومی را بصورت زیر تعریف می‌کنیم:

\(n\) : عدد کوانتومی اصلی

\(\ell\) : عدد کوانتومی مداری

\(m\) : عدد کوانتومی مغناطیسی

\(s\) : عدد کوانتومی اسپینی

آیا می‌توان مطمئن بود که همهٔ اعداد کوانتومی را پیدا کرده‌ و اندازه گرفته‌ایم؟ خیر. ممکن است کمیت‌های دیگری نیز دخیل باشند.

شواهد تجربی متعددی نتیجه‌گیری‌های کیفی فوق را تأیید می‌کند. در آینده به این شواهد خواهیم پرداخت. امّا فعلاً سعی می‌کنیم در چارچوب فرمولبندی ریاضی نظریهٔ کوانتوم و اصول موضوعهٔ آن، ترکیب سادهٔ اتم هیدروژن را بصورت کمّی مورد بررسی قرار دهیم.

توصیف کمّی اتم هیدروژن

توصیف بالا اطلاعات ذیقیمتی را در رابطه با حالات انرژی سیستم در اختیار ما می‌گذارد، اما لازم است که بصورت کمّی نیز حالات الکترون را بدست آوریم. برای اینکار به سراغ معادلهٔ شرودینگر می‌رویم. این معادله تحول زمانی سیستم را بر حسب هامیلتونی آن بدست می‌دهد. کافی است به نحوی هامیلتونی برهمکنش بین الکترون و پروتون را بنویسیم و با حل معادلهٔ شرودینگر آن دسته از حالات الکترون را که بردار آنها در فضای هیلبرت بر حسب زمان تغییر نمی‌کند (یعنی ویژه حالات هامیلتونی که همان حالات پایا را نشان می‌دهد) بدست آوریم.

معادلهٔ شرودینگر در بیان فضایی خود را می‌توان بصورت زیر نوشت: \[H\Psi(r,t)=i\hbar\frac{\partial\Psi(r,t)}{\partial t}\] که در آن عملگر \(H\) بصورت زیر بیان می‌شود: \[H=-\frac{\hbar^2}{2m}\nabla^2+V\] \( V \) پتانسیل برهمکنش است که در این مثال برهمکنش الکتریکی بین پروتون و الکترون خواهد بود. آن را کوانتیده کرده و در معادله زیر قرار می‌دهیم. \[ -\frac{\hbar^2}{2m}\nabla^2\Psi+V\Psi=i\hbar\frac{\partial\Psi}{\partial t} \] با توجه به اینکه دنبال حالات پایا هستیم، فرض می‌کنیم که تابعیت زمانی و مکانی را می‌توان از هم جدا کرد. پاسخی بصورت زیر پیشنهاد کرده و در معادله قرار می‌دهیم: \[\Psi(r,t)=\psi(r)\theta(t)\] اگر جواب را در معادله قرار دهیم و دو طرف را بر \( \Psi(r,t)\) تقسیم کنیم، خواهیم داشت: \[-\frac{\hbar^2}{2m\psi(r)}\nabla^2\psi(r)+V(r)=\frac{i\hbar}{\theta(t)}\frac{\partial\theta(t)}{\partial t}\] در اینجا چون پتانسیل برهمکنش وابستگی زاویه‌ای ندارد، آن را بصورت \( V(r)\) نوشته‌ایم. در این معادله، طرف چپ فقط به موقعیت و طرف راست تنها به زمان بستگی دارد و این تنها درصورتی امکان‌پذیر است که هر دو طرف مساوی مقداری ثابت باشند. این مقدار را \( E\) مینامیم و به دو معادلهٔ مستقل زیر می‌رسیم: \[ -\frac{\hbar^2}{2m}\nabla^2\psi(r)+V(r)\psi(r)=E \psi(r) \] و \[{i\hbar}\frac{\partial\theta(t)}{\partial t}=E\theta(t)\] جواب معادلهٔ دوم بصورت \( \exp(-i\frac{E}{\hbar} t)\) است. معادلهٔ اول را نیز با قراردادن شکل صریح \( V(r)\)باید حل کرد. دقت کنید که معادلهٔ اول را می‌توان بصورت زیر نوشت: \[ H\psi=E\psi \] اگر برای لحظاتی بیان تابعی این کمیت‌ها را فراموش کنیم، خواهیم دید که این همان رابطهٔ ویژه مقداری عملگر \( H \) است که در هر بیانی قابل استفاده است.

در مورد اتم هیدروژن، هامیلتونی بصورت زیر خواهد بود: \[H=-\frac{\hbar^2}{2\mu}\nabla^2-\frac{e^2}{4\pi\epsilon_0 r}\] پتانسیل در تشابه با مکانیک کلاسیک نوشته شده است و در آن \(\mu\) ، جرم تقلیل یافته سیستم الکترون و پروتون (یعنی \( \frac{1}{\mu}=\frac{1}{m_e}+\frac{1}{m_p}\) ) است. بدلیل تقارن موجود، دستگاه مختصات طبیعی که انتخاب می‌شود، دستگاه مختصات کروی است. شکل لاپلاسی در این مختصات بصورت زیر است: \[ \nabla^2=\frac{1}{r^2\sin\theta}\left[ \sin\theta\frac{\partial}{\partial r}\left( r^2\frac{\partial}{\partial r}\right) +\frac{\partial}{\partial\theta}\left(\sin\theta\frac{\partial}{\partial\theta}\right)+\frac{1}{\sin\phi}\frac{\partial^2}{\partial\phi^2}\right]\] با فرض اینکه وابستگی‌های زاویه‌ای و شعاعی قابل تفکیک هستند، می‌توان پاسخ را به صورت حاصلضرب یک تابع شعاعی و دو تابع زاویه‌ای نوشت: \[\psi(r,\theta,\phi)=R(r)\Theta(\theta)\Phi(\phi)\] با قراردادن این شکل از جواب در معادله و تفکیک متغیرها به سه معادله مجزا می‌رسیم.

با حل معادلهٔ قسمت شعاعی \( R(r)\) به مجموعه‌ای از توابع می رسیم که به آنها اصطلاحاً توابع وابستهٔ لاگر گفته می‌شود. این توابع یک خانواده را تشکیل می‌دهند. اعضای این خانواده با دو اندیس شماره‌گذاری می‌شوند که آنها را با \(n\) و \(\ell\) نشان می‌دهیم (\(R_{n\ell}\)). برای اینکه جوابهای همگرا داشته باشیم، مقدار اندیس دوم یعنی \(\ell\) باید بین صفر تا \(n-1\) تغییر کند.

به عنوان مثال، شکل چند عضو این خانواده بصورت زیر است: \[R_{1,0}=\left(\frac{Z}{a_0}\right)^{3/2}2 \exp(-\rho) \] \[R_{2,0}=\left(\frac{Z}{a_0}\right)^{3/2}\frac{1}{\sqrt 2} (1-\rho/2) \exp(-\rho/2)\] \[ R_{2,1}=\left(\frac{Z}{a_0}\right)^{3/2}\frac{1}{2\sqrt{6}} \rho \exp(-\rho/2)\] در اینجا \( Z\) نشان‌دهندهٔ بار هسته است که برای پروتون برابر با یک خواهد بود و \( a_0=\frac{\hbar^2 4 \pi\epsilon_0}{\mu e^2 Z}\) با واحد طول، فاصلهٔ مرجعی در مقیاس مولکولی را تعریف می‌کند که به آن «شعاع بُور» گفته می‌شود و \(\rho\) شعاع بهنجار شده نسبت به \(a_0\) و \(Z\) است، یعنی \( \rho=\frac{Z}{a_0}r\).

از توابع فوق می‌توان احتمال یافتن ذره در یک لایه کروی با شعاع بین \(r\) و \(r+dr\) را پیدا کرد. کافیست \(R_{n\ell}\) را به توان دو رسانده و در حجم لایه \(4\pi r^2 dr\) ضرب کنیم. به عبارت دیگر کمیت \( 4\pi r^2 R_{n,\ell}^2 \) احتمال یافتن الکترون در این لایهٔ کروی را بدست خواهد داد. به این احتمال «چگالی بار شعاعی» هم می‌گویند.
این تابع احتمال بازای چند تابع توزیع شعاعی مختلف در شکل روبرو (به نقل از مرجع [2]) به تصویر کشیده شده است. همانطور که دیده می شود در حالت اول یک بیشینه توزیع بار داریم که در \(\rho = 1\) اتفاق می‌افتد. حالت دوم دو بیشینه در \(\rho=0.77 \ ,\ \rho=5.24\) و حالت سوم یک بیشینه در فاصله‌ٔ \( \rho= 4\) خواهد داشت.

بخش زاویه‌ای جواب به توابعی می‌رسد که اصطلاحاً «هماهنگ‌های کروی» نامیده می‌شوند. توابعی که بخوبی بازتاب‌دهندهٔ تقارن کروی هستند و توزیع تابع را روی سطح کره‌ای به شعاع \(r\) مشخص می‌کنند. این توابع بصورت زیر تعریف می‌شوند: \[ Y_{lm}(\theta,\phi)=\sqrt{2\pi}\ \Theta_{lm}(\theta)e^{im\phi} \] توابع \( \Theta_{l,m}\)، توابع لژاندر وابسته هستند. اعضای خانوادهٔ این توابع با دو اندیس \(\ell\) و \( m \) مشخص می‌شوند. برای جوابهای همگرا، این اندیس‌ها به هم وابسته هستند. مقدار \( m\)بصورت صحیح بین \(-\ell\) تا \(+\ell\) تغییر می‌کند. چند نمونه از اعضای این خانواده در زیر دیده می‌شود: \[ \Theta_{0,0}=\frac{1}{\sqrt 2} \] \[ \Theta_{1,0}=\frac{\sqrt 6}{2}\cos \theta \] \[ \Theta_{1,\pm 1}=\frac{\sqrt 3}{2}\sin \theta \] \[\Theta_{2,0}=\frac{\sqrt{10}}{4}(3\cos^2 \theta-1) \] \[\Theta_{2,\pm 1}=\frac{\sqrt {15}}{2}\sin \theta\cos\theta \] \[\Theta_{2,\pm 2}=\frac{\sqrt {15}}{4}\sin^2 \theta \] شکل تابعیت نسبت به \(\phi\) ، ساده و بصورت \( e^{im\phi} \) است. بر این اساس شکل توابع هماهنگ کروی مشخص می‌شوند.

مجذور بخش زاویه‌ای توابع موج یعنی توابع هماهنگ کروی \( |Y_{lm}(\theta,\phi)|^2 \)، با چگالی فضایی احتمال ذره در یک پتانسیل متقارن کروی متناسب است. شکل کلّی این وابستگی‌ها در شکل روبرو (به نقل از مرجع [1]) بازای مقادیر مختلف \(\ell\) دیده می‌شود.

حاصلضرب این توابع در توابع شعاعی، شکل کلی تابع موج را بصورت \(\psi_{n\ell m}(r,\theta,\phi)\) مشخص می‌کند. بنابراین جواب کلی تابع موج، سه اندیس خواهد داشت که بصورت زیر تغییر می‌کنند: \[ n= 1, 2, 3, 4, \cdots \] \[ \ell= 0, 1, 2, \cdots, (n-1) \] \[ m=-\ell,\ -\ell+1, \cdots,\ -2,\ -1,\ 0,\ +1,\ +2,\ \cdots,\ \ell-1,\ \ell \] این سه همان اعداد کوانتومی مربوط به انرژی، اندازه حرکت زاویه‌ای و جهت اندازه حرکت زاویه‌ای هستند که به همراه اسپین، حالت الکترون را مشخص خواهند کرد. از جوابها دیده می‌شود که مقادیر هر سه کمیت گسسته هستند. یعنی انرژی الکترون هر مقداری نمی‌تواند داشته باشد و تنها مقادیر مربوط به هر \( n\) را به خود می‌گیرد که برابر است با: \[E_n=-\frac{\mu e^4}{8h^2\epsilon_0^2}\left(\frac{1}{n^2}\right)=(-13.61\ {\rm eV}) \left(\frac{1}{n^2}\right)\]

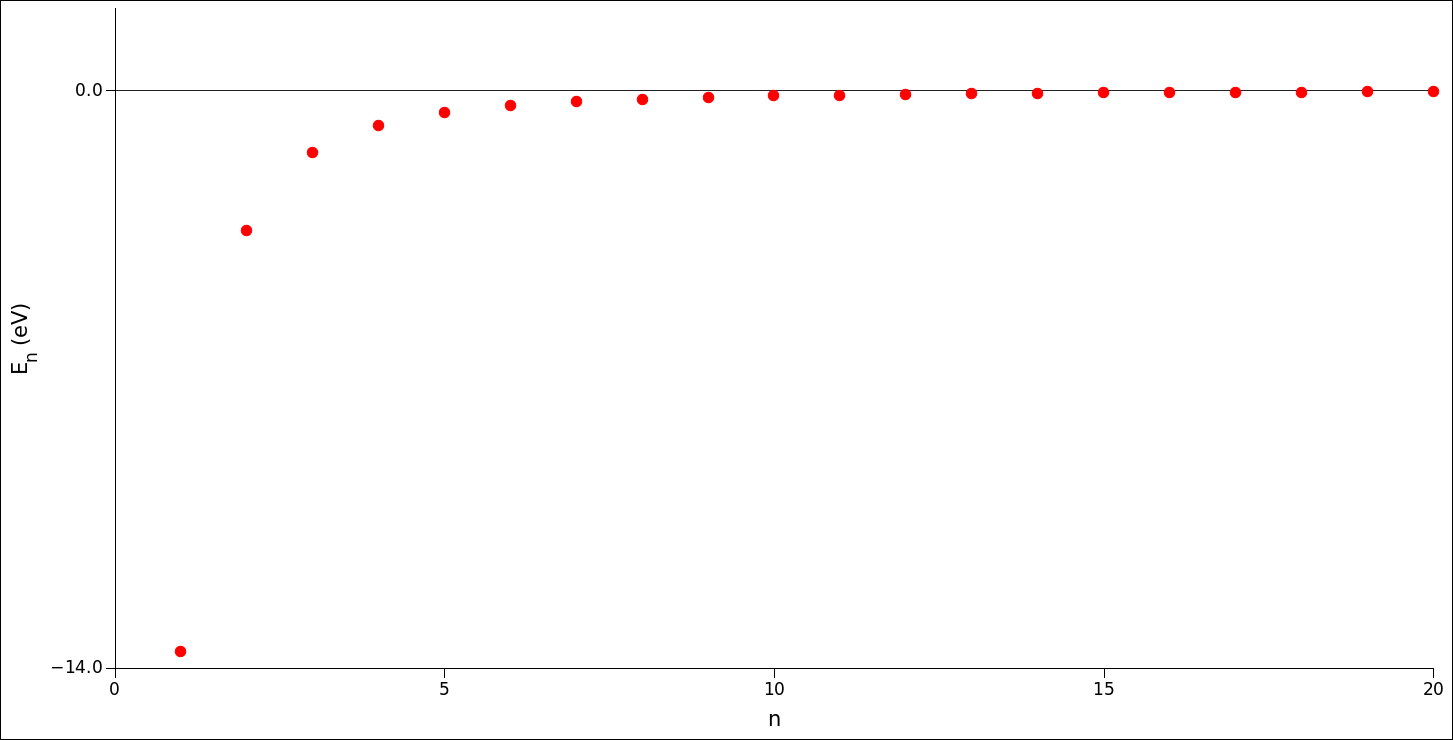حالت‌های انرژی پایا در شکل روبرو نشان داده شده است. همینطور که دیده می‌شود مقادیر انرژی‌های پایا بطور غیر یکنواخت در فاصلهٔ حداقل انرژی \( -13.6\ {\rm eV}\) که بیشترین انرژی قیدی را نشان می‌دهد تا انرژی صفر که الکترون آزاد است، توزیع شده‌اند. انرژی کمینه متناظر با حالت پایه است که به آن «حالت زمین» هم گفته می‌شود. با افزایش عدد n، انرژی قیدی به سرعت کاهش می‌یابد و بطور مجانبی به سمت صفر (الکترون آزاد) میل می‌کند.

روش دیگری که برای نمایش حالات استفاده می‌شود مشخص کردن سطح یا تراز مقادیر انرژی است که در شکل روبرو نشان داده شده‌ است. این نحوهٔ نمایش بسیار متداول است. همانطور که دیده می شود، با افزایش انرژی به سمت صفر، ترازها به هم فشرده می شوند و الکترون تقریباً هر انرژی می‌تواند داشته باشد. یعنی توزیع گسسته انرژی به توزیع پیوسته‌ای که مربوط به ذرات آزاد است نزدیک می‌شود.

اندازه حرکت زاویه‌ای هم فقط مقادیر خاصی خواهد داشت که برابر است با: \[L=\sqrt{\ell(\ell+1)}\hbar\] جهت‌گیری اندازه حرکت زاویه‌ای هم نمی‌تواند در فضا دلخواه باشد و فقط جهات گسسته‌ای را انتخاب می‌کند. اگر این جهت‌گیری را نسبت به یک محور انتخابی خاص بیان کنیم (معمولاً محور انتخابی را \( z \) می‌نامند)، برای نشان دادن جهت اندازه حرکت زاویه‌ای، می‌توان مؤلفهٔ آن را در این جهت مشخص کرد که برابر است با: \[L_z=m\hbar\] همانگونه که اشاره شد، اسپین الکترون هم باید برای توصیف حالت آن مشخص شود. رفتار ریاضی اسپین مشابه اندازه حرکت زاویه‌ای است، بنابراین مقدار آن برابر خواهد بود با: \[S=\sqrt{s(s+1)}\hbar\] چون مقدار اسپین الکترون \(s\) ثابت و برابر با ½ است، بنابراین، جهت‌گیری آن فقط دو مقدار می‌تواند داشته باشد: \[S_z=\pm s \hbar=\pm\hbar/2\] برای کامل شدن موضوع می‌توان به اسپین پروتون نیز اشاره کرد. اسپین پروتون و نوترون نیز ½ است. امّا اگر هسته متشکل از چندین ذره باشد، اسپین کل هسته ممکن است «نیمه»، «تمام» و یا صفر باشد. اگر اسپین هسته را با \( I\) و عدد کوانتومی آن را با \( i\) نشان دهیم، خواهیم داشت: \[I=\sqrt{i(i+1)}\hbar\]

روش نمایش طیف‌نگاری حالات

برای نمایش حالات مختلف الکترونی اتم‌ها، استفاده از نمایشی موسوم به نمایش طیف‌نگاری مرسوم است. در این نمایش، بجای مشخص کردن کت حالت‌ها، هر حالت با ترکیبی از اعداد و حروف مشخص می‌شود. به مجموعهٔ حالاتی که با یک انرژی (یک مقدار n) مشخص می‌شوند، اصطلاحاً «لایه» می‌گویند. لایه‌ها یا با یک حرف یا با یک عدد (همان عدد n) مشخص می‌شوند. حروف متناظر با اعداد از حرف بزرگ K شروع شده و به ترتیب الفبایی ادامه پیدا می‌کند. مثلاً لایهٔ 1 یا لایهٔ K را داریم و پس از آن به لایهٔ ۲ یا لایهٔ L می‌رسیم. در هر لایه، «زیرلایه‌»هایی متناظر با مقادیر مختلف عدد کوانتومی \(\ell\) خواهیم داشت که آنها را با حروف کوچک لاتین نمایش می‌دهیم. این حروف به ترتیب s، p، d, f هستند و پس از آن به ترتیب الفبایی ادامه پیدا می‌کنند.

نکات پایانی

• مشاهده شد که برای اتم‌های مختلف، ترازها یا سطوح انرژی متفاوتی در دسترس الکترون یا الکترون‌های سیستم خواهد بود. در مورد اتم هیدروژن، تک الکترون آن می تواند در تعداد بیشماری حالت با انرژی‌های متفاوت قرار گیرد. سئوالی که پیش می‌آید این است که الکترون در کدام یک از این حالات خواهد بود؟ آیا احتمال قرارگرفتن الکترون در هر یک از این حالات یکسان است؟ گفته می‌شود که شانس قرار گرفتن در حالت پایه یا زمین بیشتر است. چرا؟
• اگر مجموعهٔ آماری از اتم‌ها یا مولکول‌ها را در نظر بگیریم، چه اتفاقی خواهد افتاد؟ به عبارت دیگر فرض کنید تعداد زیادی اتم هیدروژن داریم. هر یک از این اتم‌ها در چه تراز انرژی‌ای قرار می‌گیرند؟ آیا همه در پایین‌ترین تراز خواهند بود؟ برای بیان این قضیه معمولاً از اصطلاح «جمعیت تراز» استفاده می‌شود، جمعیت تراز، یعنی چند مولکول، انرژی یکسان معادل انرژی آن تراز را دارند.
• جمعیت ترازها با مفهوم دمای ماکروسکوپی سیستم ارتباط پیدا می‌کند. مبنای این ارتباط چیست؟ تابع توزیع جمعیت بر اساس پارامتر دما بدست می‌آید. این توزیع چگونه است؟
• آیا جمعیت ترازها در طول زمان تغییر می‌کند؟ تحول زمانی آن چگونه است و از چه عواملی تأثیر می‌پذیرد؟
• در صورتی که اتمی در یک تراز باشد، با مختل کردن سیستم می‌توان آن را وادار کرد تا به تراز دیگری برود. این فرآیند «گذار» چگونه رخ می‌دهد و از چه عواملی تأثیر می‌پذیرد؟ آیا همهٔ گذارها امکان‌پذیر هستند؟ تأثیر این گذارها بر جمعیت ترازها چگونه است؟
• اگر مولکول چند الکترون داشته باشد، توزیع این الکترون‌ها در ترازهای انرژی آن مولکول چگونه خواهد بود؟ آیا همهٔ الکترون‌ها می‌توانند در یک تراز قرار گیرند؟
• قبلاً اشاره شد که در رفتار جمعی مولکول‌ها، ترازهای مشترک بین الکترون‌های کمتر مقید شکل می‌گیرد و نوارهای انرژی‌های مجاز ایجاد می‌شود که ناحیهٔ انرژی پیوسته‌ای را بوجود می‌آورد. در این حالت توزیع الکترون‌ها در ترازها چگونه خواهد بود؟ گذار بین نوارهای انرژی به چه طریق رخ می‌دهد؟

این سئوالات موضع مباحث بعدی است.